题目内容
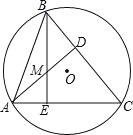
【题目】如图,△ABC内接于⊙O,AD⊥BC,BE⊥AC,AD,BE相交于点M,若AC=8,BM=4,则⊙O的半径等于( )
A.2![]() B.2
B.2![]() C.4
C.4![]() D.6
D.6
【答案】A
【解析】
试题分析:作直径AH,连接HB、HC,作OF⊥AC于F,连接CM,延长CM交AB于点N,则CN⊥AB,推出∠HCA=∠HBA=90°,证出四边形HBMC为平行四边形,求出HC,根据垂径定理求出AF,根据中位线得出OF,再根据勾股定理求出OA即可. 作直径AH,连接HB、HC,作OF⊥AC于F,连接CM,延长CM交AB于点N,则CN⊥AB,如图所示: ∵AH为直径, ∴∠HCA=∠HBA=90°, ∵CN⊥AB,BE⊥AC,
∴∠CNA=∠BEA=90° ∴∠HBA=∠CNA,∠HCA=∠BEA, ∴HB∥CN,HC∥BE, ∴四边形HBMC为平行四边形, ∴BM=HC=4, ∵OF⊥CC,OF过O, ∴根据垂径定理:CF=FA=![]() AC=4, ∵AO=OH, ∴OF为△ACH的中位线, ∴OF=
AC=4, ∵AO=OH, ∴OF为△ACH的中位线, ∴OF=![]() HC=2, ∴在Rt△AOF中,OA2=OF2+AF2=22+42=20, ∴AC=2
HC=2, ∴在Rt△AOF中,OA2=OF2+AF2=22+42=20, ∴AC=2![]() ;
;


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目