题目内容
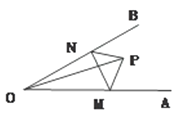
【题目】如图,点P是∠AOB内任意一点,OP=4cm,点M和点N分别是射线OA和射线OB上的动点,∠AOB=30°则△PMN周长的最小值=________ .
【答案】4cm
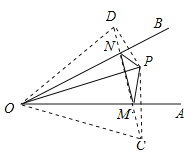
【解析】试题分析:设点P关于OA的对称点为C,关于OB的对称点为D,当点M、N在CD上时,△PMN的周长最小.
解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OP、OC、OD、PM、PN.
∵点P关于OA的对称点为C,关于OB的对称点为D,
∴PM=CM,OP=OC,∠COA=∠POA;
∵点P关于OB的对称点为D,
∴PN=DN,OP=OD,∠DOB=∠POB,
∴OC=OD=OP=4cm,
∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,
∴△COD是等边三角形,
∴CD=OC=OD=4cm.
∴△PMN的周长的最小值=PM+MN+PN=CM+MN+DN=CD=4cm.
故答案为4cm.

练习册系列答案
相关题目