题目内容
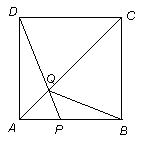
如图1,将三角板放在正方形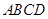 上,使三角板的直角顶点
上,使三角板的直角顶点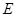 与正方形
与正方形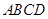 的顶点
的顶点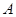 重合,三角扳的一边交
重合,三角扳的一边交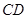 于点
于点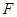 .另一边交
.另一边交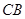 的延长线于点
的延长线于点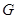 .
.
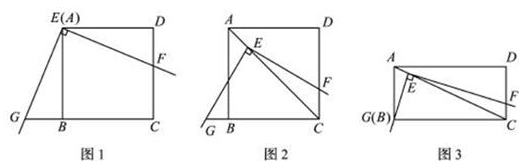
(1)求证: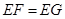 ;
;
(2)如图2,移动三角板,使顶点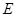 始终在正方形
始终在正方形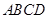 的对角线
的对角线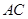 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形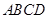 ”改为“矩形
”改为“矩形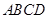 ”,且使三角板的一边经过点
”,且使三角板的一边经过点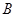 ,其他条件不变,若
,其他条件不变,若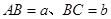 ,求
,求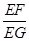 的值.
的值.
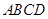 上,使三角板的直角顶点
上,使三角板的直角顶点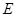 与正方形
与正方形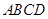 的顶点
的顶点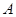 重合,三角扳的一边交
重合,三角扳的一边交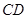 于点
于点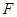 .另一边交
.另一边交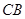 的延长线于点
的延长线于点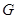 .
.
(1)求证:
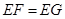 ;
;(2)如图2,移动三角板,使顶点
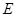 始终在正方形
始终在正方形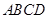 的对角线
的对角线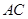 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:(3)如图3,将(2)中的“正方形
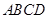 ”改为“矩形
”改为“矩形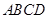 ”,且使三角板的一边经过点
”,且使三角板的一边经过点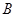 ,其他条件不变,若
,其他条件不变,若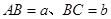 ,求
,求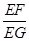 的值.
的值. (1)见解析
(2)成立.
(3)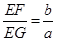 .
.
(2)成立.
(3)
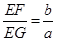 .
.(1)由∠GEB+∠BEF=90°,∠DEF+∠BEF=90°,得∠DEF=∠GEB,再有ED=BE,即证得Rt△FED≌Rt△GEB,则EF=EG;
(2)过点E分别作BC、CD的垂线,垂足分别为H、I,则EH=EI,∠HEI=90°,由∠GEH+∠HEF=90°,∠IEF+∠HEF=90°,得∠IEF=∠GEH,即可证得Rt△FEI≌Rt△GEH,则EF=EG;
(3)过点E分别作BC、CD的垂线,垂足分别为M、N,∠MEN=90°,则EM∥AB,EN∥AD,即得△CEN∽△CAD,△CEM∽△CAB,根据相似三角形的对应边成比例可得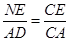 ,
, ,即得
,即得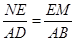 ,从而可得
,从而可得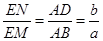 =
=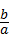 ,再证得△GME∽△FNE即可得到结果。
,再证得△GME∽△FNE即可得到结果。
(2)过点E分别作BC、CD的垂线,垂足分别为H、I,则EH=EI,∠HEI=90°,由∠GEH+∠HEF=90°,∠IEF+∠HEF=90°,得∠IEF=∠GEH,即可证得Rt△FEI≌Rt△GEH,则EF=EG;
(3)过点E分别作BC、CD的垂线,垂足分别为M、N,∠MEN=90°,则EM∥AB,EN∥AD,即得△CEN∽△CAD,△CEM∽△CAB,根据相似三角形的对应边成比例可得
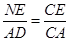 ,
, ,即得
,即得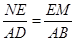 ,从而可得
,从而可得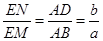 =
=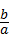 ,再证得△GME∽△FNE即可得到结果。
,再证得△GME∽△FNE即可得到结果。
练习册系列答案
相关题目
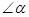 的度数是
的度数是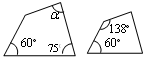
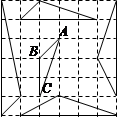
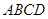 中,点
中,点 在
在 上从
上从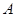 向
向 运动,连接
运动,连接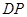 交
交
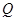 .
.
 ≌△
≌△ ;
;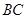 上运动到点
上运动到点 ,在整个运动过程中,当点
,在整个运动过程中,当点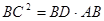 .
.
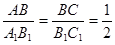 ,且∠B=∠B1=56°,则
,且∠B=∠B1=56°,则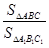 = 。
= 。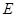 是矩形
是矩形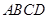 的边
的边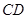 上一点,
上一点, 于
于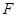 ,试说明:
,试说明: .
.