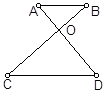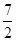题目内容
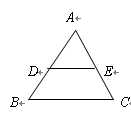
如图,在边长为4的正方形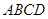 中,点
中,点 在
在 上从
上从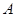 向
向 运动,连接
运动,连接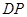 交
交
于点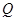 .
.
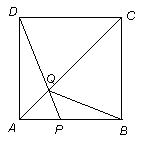
⑴试证明:无论点 运动到
运动到 上何处时,都有△
上何处时,都有△ ≌△
≌△ ;
;
⑵当点 在
在 上运动到什么位置时,△
上运动到什么位置时,△ 的面积是正方形
的面积是正方形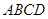 面积的
面积的 ;
;
⑶若点 从点
从点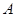 运动到点
运动到点 ,再继续在
,再继续在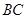 上运动到点
上运动到点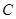 ,在整个运动过程中,当点
,在整个运动过程中,当点 运动到什么位置时,△
运动到什么位置时,△ 恰为等腰三角形.
恰为等腰三角形.
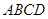 中,点
中,点 在
在 上从
上从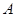 向
向 运动,连接
运动,连接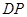 交
交
于点
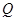 .
.
⑴试证明:无论点
 运动到
运动到 上何处时,都有△
上何处时,都有△ ≌△
≌△ ;
;⑵当点
 在
在 上运动到什么位置时,△
上运动到什么位置时,△ 的面积是正方形
的面积是正方形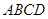 面积的
面积的 ;
;⑶若点
 从点
从点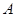 运动到点
运动到点 ,再继续在
,再继续在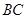 上运动到点
上运动到点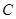 ,在整个运动过程中,当点
,在整个运动过程中,当点 运动到什么位置时,△
运动到什么位置时,△ 恰为等腰三角形.
恰为等腰三角形.⑴证明:在正方形 中,无论点
中,无论点 运动到
运动到 上何处时,都有
上何处时,都有
 =
= ∠
∠ =∠
=∠
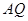 =
=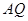 ∴△
∴△ ≌△
≌△
⑵△ 的面积恰好是正方形ABCD面积的
的面积恰好是正方形ABCD面积的 时,
时,
过点Q作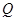
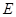 ⊥
⊥ 于
于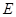 ,
, ⊥
⊥ 于
于 ,
,
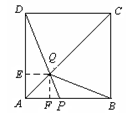
则 =
= 

 =
= =
= ∴
∴ =
=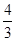
由△ ∽△
∽△ 得
得 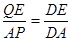 解得
解得
∴ 时,△
时,△ 的面积是正方形
的面积是正方形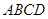 面积的
面积的
⑶若△ 是等腰三角形,则有
是等腰三角形,则有  =
= 或
或 =
= 或
或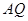 =
=
①当点 运动到与点
运动到与点 重合时,由四边形
重合时,由四边形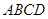 是正方形知
是正方形知  =
=
此时△ 是等腰三角形
是等腰三角形
②当点 与点
与点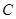 重合时,点
重合时,点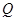 与点
与点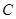 也重合,此时
也重合,此时 =
= , △
, △ 是等腰三角形
是等腰三角形
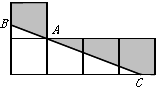
③:如图,
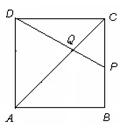
设点 在
在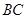 边上运动到
边上运动到 时,有
时,有 =
=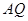
∵ ∥
∥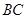 ∴∠
∴∠ =∠
=∠
又∵∠ =∠
=∠ ∠
∠ =∠
=∠
∴∠ =∠
=∠ ∴
∴ 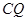 =
=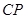 =
=
∵ =
=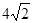
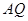 =
=  =4 ∴
=4 ∴
即当 时,△
时,△ 是等腰三角形.
是等腰三角形.
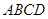 中,无论点
中,无论点 运动到
运动到 上何处时,都有
上何处时,都有 =
= ∠
∠ =∠
=∠
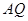 =
=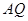 ∴△
∴△ ≌△
≌△
⑵△
 的面积恰好是正方形ABCD面积的
的面积恰好是正方形ABCD面积的 时,
时,过点Q作
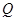
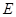 ⊥
⊥ 于
于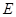 ,
, ⊥
⊥ 于
于 ,
,
则
 =
= 

 =
= =
= ∴
∴ =
=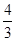
由△
 ∽△
∽△ 得
得 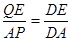 解得
解得
∴
 时,△
时,△ 的面积是正方形
的面积是正方形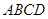 面积的
面积的
⑶若△
 是等腰三角形,则有
是等腰三角形,则有  =
= 或
或 =
= 或
或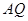 =
=
①当点
 运动到与点
运动到与点 重合时,由四边形
重合时,由四边形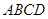 是正方形知
是正方形知  =
=
此时△
 是等腰三角形
是等腰三角形②当点
 与点
与点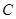 重合时,点
重合时,点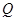 与点
与点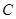 也重合,此时
也重合,此时 =
= , △
, △ 是等腰三角形
是等腰三角形③:如图,

设点
 在
在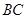 边上运动到
边上运动到 时,有
时,有 =
=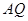
∵
 ∥
∥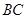 ∴∠
∴∠ =∠
=∠
又∵∠
 =∠
=∠ ∠
∠ =∠
=∠
∴∠
 =∠
=∠ ∴
∴ 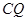 =
=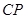 =
=
∵
 =
=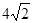
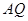 =
=  =4 ∴
=4 ∴
即当
 时,△
时,△ 是等腰三角形.
是等腰三角形.(1)两边一角 AQ="AQ" ,AB=AD=4,∠DAQ=∠BAQ=45度所以两个三角形全等。
(2)做QE垂直于AD,△DQE相似于△DPA,△ADQ面积=AD QE/2,正方形面积=AD
QE/2,正方形面积=AD AB,△ ADQ的面积是正方形面积的1/6,则QE=AB/3=4/3,△AQE是等腰直角三角形,则AQ=QE=4/3,DQ=AD-AQ=8/3,△DQE相似△DPA中, DQ/AD=QE/AP,带入数据得:8/3 /4=" 4/3" /AP,故AP=2,因为AB="4" 则P点正好运动到AB的中点
AB,△ ADQ的面积是正方形面积的1/6,则QE=AB/3=4/3,△AQE是等腰直角三角形,则AQ=QE=4/3,DQ=AD-AQ=8/3,△DQE相似△DPA中, DQ/AD=QE/AP,带入数据得:8/3 /4=" 4/3" /AP,故AP=2,因为AB="4" 则P点正好运动到AB的中点
(3)假设△ADQ恰好为等腰三角形::P在 ABC上运动首先当AD=QD=4时 Q与C点刚好重合所以P运动到C点△ADQ为等腰三角形;当P运动到B点时,AQ="QD" △ADQ为等腰直角三角形;当AD=AQ=4时,△ADQ与△CPQ相似,则PC=CQ=AC-AQ=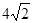 -4,则P运动到距离C点
-4,则P运动到距离C点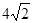 -4时,△ADQ为等腰三角形
-4时,△ADQ为等腰三角形
(2)做QE垂直于AD,△DQE相似于△DPA,△ADQ面积=AD
 QE/2,正方形面积=AD
QE/2,正方形面积=AD AB,△ ADQ的面积是正方形面积的1/6,则QE=AB/3=4/3,△AQE是等腰直角三角形,则AQ=QE=4/3,DQ=AD-AQ=8/3,△DQE相似△DPA中, DQ/AD=QE/AP,带入数据得:8/3 /4=" 4/3" /AP,故AP=2,因为AB="4" 则P点正好运动到AB的中点
AB,△ ADQ的面积是正方形面积的1/6,则QE=AB/3=4/3,△AQE是等腰直角三角形,则AQ=QE=4/3,DQ=AD-AQ=8/3,△DQE相似△DPA中, DQ/AD=QE/AP,带入数据得:8/3 /4=" 4/3" /AP,故AP=2,因为AB="4" 则P点正好运动到AB的中点(3)假设△ADQ恰好为等腰三角形::P在 ABC上运动首先当AD=QD=4时 Q与C点刚好重合所以P运动到C点△ADQ为等腰三角形;当P运动到B点时,AQ="QD" △ADQ为等腰直角三角形;当AD=AQ=4时,△ADQ与△CPQ相似,则PC=CQ=AC-AQ=
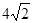 -4,则P运动到距离C点
-4,则P运动到距离C点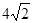 -4时,△ADQ为等腰三角形
-4时,△ADQ为等腰三角形
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
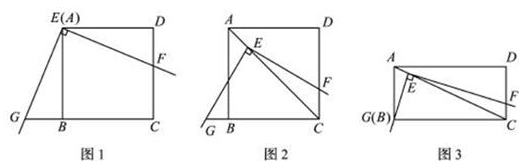
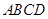 上,使三角板的直角顶点
上,使三角板的直角顶点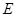 与正方形
与正方形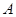 重合,三角扳的一边交
重合,三角扳的一边交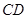 于点
于点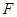 .另一边交
.另一边交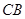 的延长线于点
的延长线于点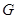 .
.
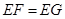 ;
;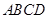 的对角线
的对角线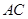 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由: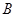 ,其他条件不变,若
,其他条件不变,若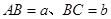 ,求
,求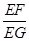 的值.
的值.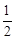 ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.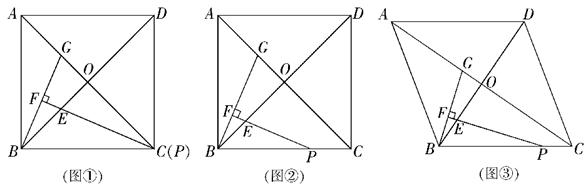
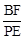 = ,并结合图②证明你的猜想;(5分)
= ,并结合图②证明你的猜想;(5分) ,
, ,以原点为位似中心,相似比为1∶3.把线段
,以原点为位似中心,相似比为1∶3.把线段 缩小,则过
缩小,则过 点对应点的反比例函数的解析式为( )
点对应点的反比例函数的解析式为( )