题目内容
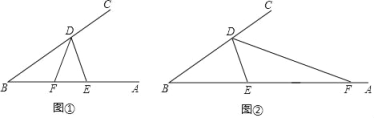
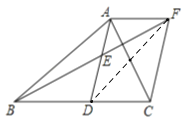
【题目】已知:在![]() 中,
中,![]() 是
是![]() 边上的中线,点
边上的中线,点![]() 是
是![]() 的中点;过点
的中点;过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 分别满足什么条件时,四边形
分别满足什么条件时,四边形![]() 是菱形;四边形
是菱形;四边形![]() 是矩形,并说明理由.
是矩形,并说明理由.
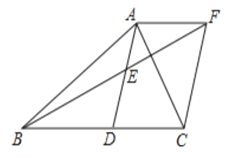
【答案】(1)见详解;(2)①当![]() 时,四边形
时,四边形![]() 是矩形;②当
是矩形;②当![]() ,四边形
,四边形![]() 是菱形.
是菱形.
【解析】
(1)先证明![]() ,然后由全等三角形的性质,得到BD=CD=AF,即可证明结论成立;
,然后由全等三角形的性质,得到BD=CD=AF,即可证明结论成立;
(2)①根据矩形的判定定理即可得到结论;②根据菱形的判定定理即可得到结论.
(1)证明:
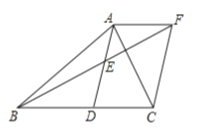
∵![]() ,∴
,∴![]() ,
,
在![]() 和
和![]() 中
中
∵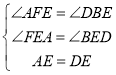
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴四边形![]() 为平行四边形;
为平行四边形;
(2)①当![]() 时,四边形
时,四边形![]() 是矩形;
是矩形;
由(1)可知,![]() ,
,![]() ,
,
∴四边形ABDF是平行四边形,
∴AB=DF,
∴AB=AC=DF,
∴平行四边形ADCF是矩形;
②当![]() ,四边形
,四边形![]() 是菱形;
是菱形;
由①可知,四边形ABDF是平行四边形,
∴AB∥DF,
∵![]() ,即AB⊥AC,
,即AB⊥AC,
∴DF⊥AC,
∴平行四边形ADCF是菱形.

练习册系列答案
相关题目