题目内容
【题目】如图，已知四边形ABCD的顶点为A（1，2），B（﹣1，2），C，（﹣1，﹣2），D（1，﹣2），点M和点N同时从E点出发，沿四边形的边做环绕匀速运动，M点以1单位/s的速度做逆时针运动，N点以2单位/s的速度做顺时针运动，则点M和点N第2019次相遇时的坐标为_____．
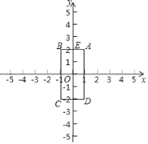
【答案】（0,2）；
【解析】
由点
、
、
、
的坐标可得出
、
的长度，设点
和点
第2019次相遇时的时间为
，根据第一次相遇的路程和=周长，所以第2019次相遇的路程和=周长×2019，即可得出关于的一元一次方程，解之即可得出的值，再根据路程=速度×时间可求出和点第2019次相遇时，点走过的路程，结合矩形的周长为
，即可找出点和点第2019次相遇时的坐标，此题得解.
，
，
，
，
，
，
设点和点第2019次相遇时的时间为，
根据题意得：
，
解得：
，
点和点第2019年相遇时，点走过的路程为，
矩形
的周长为，
，
点和点第2019次相遇时的位置在点
处.
故答案为：
.
练习册系列答案
相关题目
【题目】小明根据学习函数的经验，对函数y＝|x|+2的图象与性质进行了研究，下面是小明的研究过程，请补充完成．
（1）函数y＝|x|+2的自变量x的取值范围是 ；
（2）列表，把表格填写完整：
x | …… | ﹣2 | ﹣1 | 0 | 1 | 2 | …… |
y | …… |
|
|
|
|
| …… |
（3）在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
（4）写出该函数的两条性质．
