题目内容
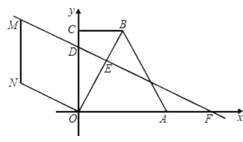
【题目】如图,矩形OABC在平面直角坐标系中,点A在y轴上,点C在![]() 轴上,OC=4,直线
轴上,OC=4,直线![]() 经过点A,交
经过点A,交![]() 轴于点D,点E在线段BC上,ED⊥AD.
轴于点D,点E在线段BC上,ED⊥AD.
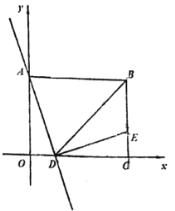
(1)求点E的坐标;
(2)联结BD,求cot∠BDE的值;
(3)点G在直线BC,且∠EDG=45°,求点G的坐标.
【答案】(1)(4,1);(2)2;(3)(4,![]() )或(4,6).
)或(4,6).
【解析】
(1)先求出OA、OD、DC的长度,再证明△AOD≌△DCE,从而得出EC=OD,即可求出E点坐标;(2)作EQ⊥BD,根据等腰三角形的性质可求DQ和EQ的长度,即可求出cot∠BDE;(3)分G在C点下方和B点上方两种情况讨论,借助三角形的相似即可求出相应线段的长,从而求出点的坐标.
(1)∵![]() 经过点A,点A在y轴上,
经过点A,点A在y轴上,
∴A(0,3),即OA=3
当y=0时,![]() ,解得x=1
,解得x=1
∴D(1,0),即OD=1
∵矩形OABC中OC=4,
∴OB=OA=3,DC=OC-OD=3
∠AOC=∠BCD=90°.
∴∠OAD+∠ADO=90°
∵ED⊥AD
∴∠EDC+∠ADO=90°
∴∠EDC=∠OAD
又∵OA=CD=3
∴△AOD≌△DCE(ASA)
∴CE=OD=1
∴E(4,1).
(2)过点E作EQ⊥BD,与BD相交于Q.
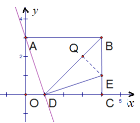
∵DC=BC=3,∠BCD=90°,
∴△BCD为等腰直角三角形,
∴BD=![]() ,∠DBC=45°
,∠DBC=45°
∵EQ⊥BD
∴△EBQ为等腰直角三角形
∵CE=1
∴BE=BC-CE=2
∴BQ=QE=![]()
∴QD=![]()
∴![]()
(3)如图①当G点在C点上方时
∵∠EDG=45°=∠EDC+∠GDC
∠BDC=45°= ∠BDE +∠EDC
∴∠GDC=∠BDE
∴Rt△GCD∽Rt△EQD
∴![]()
即![]()
解得GC=![]()
故G(4,![]() );
);
②当G‘点在B点上方时
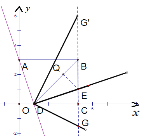
∵∠DG‘C+∠G‘DB=∠DBC=45°
∠G‘DB+∠BDE=∠EDG‘=45°
∴∠DG‘C=∠BDE
∵∠DBC=∠EDG‘ =45°
∴△DEG‘∽△BED
∴![]()
∵![]() ,BE=2,
,BE=2,
∴EG‘=5
∴CG‘=6即G‘(4,6)
故G点坐标为(4,![]() )或(4,6).
)或(4,6).

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案