题目内容
【题目】如图,在平面直角坐标系中,点A(1, ![]() ),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( )
),点B(2,0),P为线段OB上一点,过点P作PQ∥OA,交AB于点Q,连接AP,则△APQ面积最大值为( ) 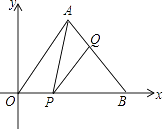
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:如图,作AF⊥OB于F,QE⊥OB于E.设OP=x, 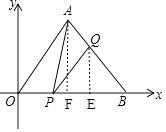 ,
,
∵点A(1, ![]() ),点B(2,0),
),点B(2,0),
∴点F是OB的中点,
∴OF=2÷2=1,AF= ![]() ,
,
∵OF=FB,AF⊥OB,
∴AO=AB,
∴OA=AB= ![]() =2,
=2,
∵OA=AB=OB=2,
∴△AOB是等边三角形,
∴∠BOA=∠BAO=∠ABO=60°,
∵PQ∥OA,
∴∠QPB=∠AOB=60°,
∴△BPQ是等边三角形,
∴BP=BQ=PQ=2﹣x,
∴S△BPQ= ![]() (2﹣x)2 ,
(2﹣x)2 ,
∴S△APQ=S△AOB﹣S△AOP﹣S△BPQ
= ![]() ×22﹣
×22﹣ ![]() x
x ![]() ﹣
﹣ ![]() (2﹣x)2
(2﹣x)2
= ![]() ﹣
﹣ ![]() x﹣
x﹣ ![]() ×(4﹣2x+x2)
×(4﹣2x+x2)
=﹣ ![]() (x﹣1)2+
(x﹣1)2+ ![]() ,
,
≤ ![]()
∴当x=1时,△APQ面积最大值为 ![]() .
.
故选:B.
【考点精析】关于本题考查的二次函数的最值和相似三角形的判定与性质,需要了解如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

【题目】七(1)班小明同学通过《测量硬币的厚度与质量》实验得到了每枚硬币的厚度和质量,数据如下表.他从储蓄罐取出一把5角和1元硬币,为了知道总的金额,他把这些硬币叠起来,用尺量出它们的总厚度为22.6mm,又用天平称出总质量为78.5g,请你帮助小明同学算出这把硬币的总金额为______元.
1元硬币 | 5角硬币 | |
每枚厚度(单位:mm) | 1.8 | 1.7 |
每枚质量(单位:g) | 6.1 | 6.0 |
【题目】某公司有![]() 、
、![]() 两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
两种型号的客车共20辆,它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下,共载客720人.
A型号客车 | B型号客车 | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 600 | 450 |
(1)求![]() 、
、![]() 两种型号的客车各有多少辆?
两种型号的客车各有多少辆?
(2)某中学计划租用![]() 、
、![]() 两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?
两种型号的客车共8辆,同时送七年级师生到沙家浜参加社会实践活动,已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车?