题目内容
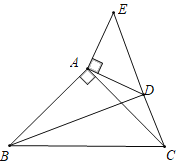
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的动点(不与
边上的动点(不与![]() 重合),点
重合),点![]() 在
在![]() 边上,并且满足
边上,并且满足![]() .
.
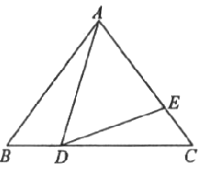
(1)求证:![]() ;
;
(2)若![]() 的长为
的长为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)当(2)中的![]() 最短时,求
最短时,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由等腰三角形的性质可得![]() ,然后根据三角形的外角性质可得
,然后根据三角形的外角性质可得![]() ,进而可证得结论;
,进而可证得结论;
(2)根据相似三角形的对应边成比例可得CE与x的关系,进一步即可得出结果;
(3)根据(2)题的结果,利用二次函数的性质可得AE最短时x的值,即BD的长,进而可得AD的长和△ADC的面积,进一步利用所求三角形的面积与△ADC的面积之比等于AE与AC之比即得答案.
解:(1)∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ;
;
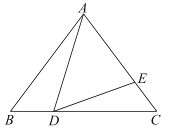
(2)∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ;
;
(3)∵![]() ,∴
,∴![]() 时,
时,![]() 的值最小为6.4,此时
的值最小为6.4,此时![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目