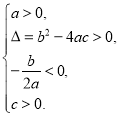题目内容
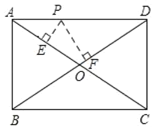
【题目】问题背景:如图1设P是等边△ABC内一点,PA=6,PB=8,PC=10,求∠APB的度数.小君研究这个问题的思路是:将△ACP绕点A逆时针旋转60°得到△ABP',易证:△APP'是等边三角形,△PBP'是直角三角形,所以∠APB=∠APP'+∠BPP'=150°.

简单应用:(1)如图2,在等腰直角△ABC中,∠ACB=90°.P为△ABC内一点,且PA=5,PB=3,PC=2![]() ,则∠BPC= °.
,则∠BPC= °.
(2)如图3,在等边△ABC中,P为△ABC内一点,且PA=5,PB=12,∠APB=150°,则PC= .
拓展廷伸:(3)如图4,∠ABC=∠ADC=90°,AB=BC.求证:![]() BD=AD+DC.
BD=AD+DC.
(4)若图4中的等腰直角△ABC与Rt△ADC在同侧如图5,若AD=2,DC=4,请直接写出BD的长.

【答案】(1)135;(2)13;(3)见解析;(4)![]()
【解析】
简单应用:(1)先利用旋转得出BP'=AP=5,∠PCP'=90°,CP'=CP=2![]() ,再根据勾股定理得出PP'=
,再根据勾股定理得出PP'=![]() CP=4,最后用勾股定理的逆定理得出△BPP'是以BP'为斜边的直角三角形,即可得出结论;
CP=4,最后用勾股定理的逆定理得出△BPP'是以BP'为斜边的直角三角形,即可得出结论;
(2)同(1)的方法得出∠APP'=60°,进而得出∠BPP'=∠APB﹣∠APP'=90°,最后用勾股定理即可得出结论;
拓展廷伸:(3)先利用旋转得出BD'=BD,CD'=AD,∠BCD'=∠BAD,再判断出点D'在DC的延长线上,最后用勾股定理即可得出结论;
(4)先利用旋转得出BD'=BD,CD=AD',∠DBD'=90°,∠BCD=∠BAD',再判断出点D'在AD的延长线上,最后用勾股定理即可得出结论.
解:简单应用:(1)如图2,
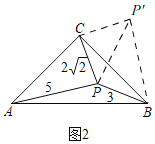
∵△ABC是等腰直角三角形,
∴∠ACB=90°,AC=BC,将
△ACP绕点C逆时针旋转90°得到△CBP',连接PP',
∴BP'=AP=5,∠PCP'=90°,CP'=CP=2![]() ,
,
∴∠CPP'=∠CP'P=45°,
根据勾股定理得,PP'=![]() CP=4,
CP=4,
∵BP'=5,BP=3,∴PP'2+BP2=BP',
∴△BPP'是以BP'为斜边的直角三角形,
∴∠BPP'=90°,
∴∠BPC=∠BPP'+∠CPP'=135°,
故答案为:135;
(2)如图3,

∵△ABC是等边三角形,
∴∠BAC=60°,AC=AB,
将△ACP绕点A逆时针旋转60°得到△ABP',连接PP',
∴BP'=CP,AP'=AP=5,∠PAP'=60°,
∴△APP'是等边三角形,
∴PP'=AP=5,∠APP'=60°,
∵∠APB=150°,
∴∠BPP'=∠APB﹣∠APP'=90°,
根据勾股定理得,BP'=![]() =13,
=13,
∴CP=13,
故答案为:13;
拓展廷伸:(3)如图4,
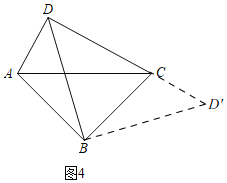
在△ABC中,∠ABC=90°,AB=BC,
将△ABD绕点B顺时针旋转90°得到△BCD',
∴BD'=BD,CD'=AD,∠BCD'=∠BAD,
∵∠ABC=∠ADC=90°,
∴∠BAD+∠BCD=180°,
∴∠BCD+∠BCD'=180°,
∴点D'在DC的延长线上,
∴DD'=CD+CD'=CD+AD,
在Rt△DBD'中,DD'=![]() BD,
BD,
∴![]() BD=CD+AD;
BD=CD+AD;
(4)如图5,

在△ABC中,∠ABC=90°,AB=BC,
连接BD,将△CBD绕点B顺时针旋转90°得到△ABD',
∴BD'=BD,CD=AD',∠DBD'=90°,∠BCD=∠BAD',
AB与CD的交点记作G,
∵∠ADC=∠ABC=90°,
∴∠DAB+∠AGD=∠BCD+∠BGC=180°,
∵∠AGD=∠BGC,
∴∠BAD=∠BCD,
∴∠BAD=∠BAD',
∴点D'在AD的延长线上,
∴DD'=AD'﹣AD=CD﹣AD=2,
在Rt△BDD'中,BD=![]() DD'=
DD'=![]() .
.

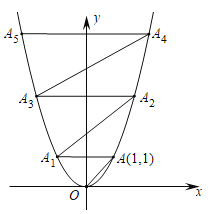
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
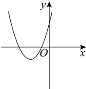
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.