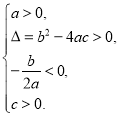题目内容
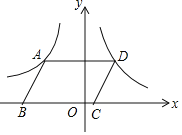
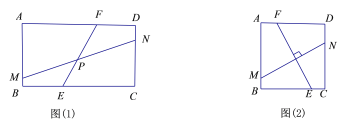
【题目】如图,AN是⊙O的直径,四边形ABMN是矩形,与圆相交于点E,AB=15,D是⊙O上的点,DC⊥BM,与BM交于点C,⊙O的半径为R=30.
(1)求BE的长.
(2)若BC=15,求![]() 的长.
的长.

【答案】(1)30﹣15![]() ;(2)15π
;(2)15π
【解析】
(1)连接OE,过O作OF⊥BM于F,在Rt△OEF中,由勾股定理得出EF的长,进而求得EB的长.
(2)连接OD,则在直角三角形ODQ中,可求得∠QOD=60°,过点E作EH⊥AO于H,在直角三角形OEH中,可求得∠EOH=30°,则得出![]() 的长度.
的长度.
解:(1)连接OE,过O作OF⊥BM于F,则四边形ABFO是矩形,
∴FO=AB=15,BF=AO,
在Rt△OEF中,EF=![]() =15
=15![]() ,
,
∵BF=AO=30,
∴BE=30﹣15![]() .
.
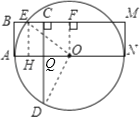
(2)连接OD,在直角三角形ODQ中,
∵OD=30,OQ=30﹣15=15,
∴∠ODQ=30°,
∴∠QOD=60°,
过点E作EH⊥AO于H,在直角三角形OEH中,
∵OE=30,EH=15,
∴![]() ,
,
∴∠EOH=30°,
∴∠DOE=90°,
∴![]() =
=![]() π60=15π.
π60=15π.

练习册系列答案
相关题目
【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
方程两根的情况 | 对应的二次函数的大致图象 |
|
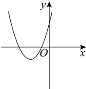
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.