题目内容
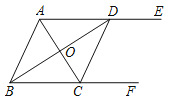
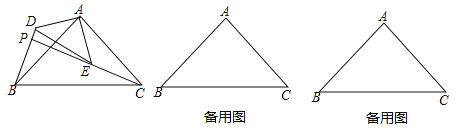
【题目】如图,在![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 以每秒3个单位长的速度运动至点
以每秒3个单位长的速度运动至点![]() ,过点
,过点![]() 作
作![]() 射线
射线![]() 于点
于点![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒(
秒(![]() ).
).
(1)线段![]() 的长为 (用含
的长为 (用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 与
与![]() 的周长的比为
的周长的比为![]() 时,求
时,求![]() 的值.
的值.
(3)设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当直线![]() 把
把![]() 分成的两部分图形中有一个是轴对称图形时,直接写出
分成的两部分图形中有一个是轴对称图形时,直接写出![]() 的值.
的值.

【答案】(1) ![]() 或
或![]() ;(2)
;(2)![]() ;(3)
;(3)![]() (
(![]() )或
)或![]() (
(![]() );(4)
);(4)![]() 秒或2秒.
秒或2秒.
【解析】
(1)先在![]() 中求出
中求出![]() ,再在
,再在![]() 中求出
中求出![]() ,最后用勾股定理即可得出结论;
,最后用勾股定理即可得出结论;
(2)由相似三角形的周长的比等于相似比得出方程,解方程即可;
(3)分两种情况,由三角形面积公式和相似三角形的性质即可得出答案;
(4)分两种情况讨论计算,由轴对称图形的定义,用相等的线段建立方程求解即可.
解:(1)在![]() 中,
中,![]() ,
,
由题意得,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
根据勾股定理得,![]() .
.
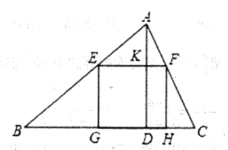
当![]() 时,如图1所示:
时,如图1所示:
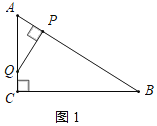
![]() ;
;
当![]() 时,如图2所示:
时,如图2所示:
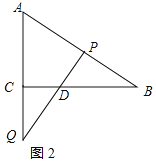
![]() ;
;
故答案为:![]() 或
或![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
即当![]() 与
与![]() 的周长的比为
的周长的比为![]() 时,
时,![]() 为
为![]() 秒.
秒.
(3)分两种情况:
①当![]() 时,如图1所示:
时,如图1所示:
![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ;
;
即![]() (
(![]() );
);
②当![]() 时,如图2所示:
时,如图2所示:
由(1)得:![]() ,
,
同(2)得:![]() ,
,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]()
![]() ;
;
即![]() (
(![]() );
);
(4)由(1)知,![]() ,
,![]() 或
或![]() ,
,
当![]() 时,四边形
时,四边形![]() 是轴对称图形,
是轴对称图形,
则![]() ,
,
∴![]() ;
;
当![]() 时,设
时,设![]() 和
和![]() 相交于
相交于![]() ,
,
当![]() 时,四边形
时,四边形![]() 是轴对称图形,
是轴对称图形,
则![]() ,
,
∴![]() .
.
综上所述,当直线![]() 把
把![]() 分成的两部分图形中有一个是轴对称图形时,
分成的两部分图形中有一个是轴对称图形时,![]() 的值为
的值为![]() 秒或2秒.
秒或2秒.

【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查部分学生的数学成绩,并将抽样的数据进行了如下整理:
①如下分数段整理样本;
等级等级 | 分数段 | 各组总分 | 人数 |
A | 110<X<120 | P | 4 |
B | 100<X<110 | 843 | n |
C | 90<X≤100 | 574 | m |
D | 80<X<90 | 171 | 2 |
②根据左表绘制扇形统计图.

(1)填空m= ,n= ,数学成绩的中位数所在的等级 ;
(2)如果该校有1200名学生参加了本次模拟测,估计D等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A等级学生的数学成绩的平均分数.