题目内容
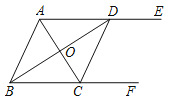
【题目】如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADB=30°,BD=6,求AD的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由平行线的性质和角平分线定义得出∠ABD=∠ADB,证出AB=AD,同理:AB=BC,得出AD=BC,证出四边形ABCD是平行四边形,即可得出结论;
(2)由菱形的性质得出AC⊥BD,OD=OB=![]() BD=3,再由三角函数即可得出AD的长.
BD=3,再由三角函数即可得出AD的长.
试题解析:(1)证明:∵AE∥BF,∴∠ADB=∠CBD,又∵BD平分∠ABF,∴∠ABD=∠CBD,∴∠ABD=∠ADB,∴AB=AD,同理:AB=BC,∴AD=BC,∴四边形ABCD是平行四边形,又∵AB=AD,∴四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,BD=6,∴AC⊥BD,OD=OB=![]() BD=3,∵∠ADB=30°,∴cos∠ADB=
BD=3,∵∠ADB=30°,∴cos∠ADB=![]() ,∴AD=
,∴AD=![]() =
=![]() .
.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目