题目内容
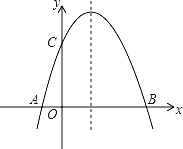
【题目】如图,在平面直角坐标系xOy中,顶点为M的抛物线![]() 经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
经过点A和x轴正半轴上的点B,AO=OB=2,∠AOB=1200.
(1)求这条抛物线的表达式;
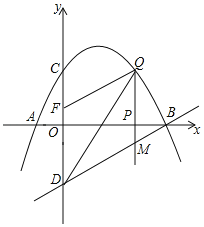
(2)连接OM,求∠AOM的大小;
(3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
【答案】解:(1)![]() .
.
(2)150°.
(3)C的坐标为(4,0)或(8,0).
【解析】
(1)应用三角函数求出点A的坐标,将A,B的坐标代入![]() ,即可求得a、b,从而求得抛物线的表达式.
,即可求得a、b,从而求得抛物线的表达式.
(2)应用二次函数的性质,求出点M的坐标,从而求得![]() ,进而求得∠AOM的大小.
,进而求得∠AOM的大小.
(3)由于可得![]() ,根据相似三角形的判定,分
,根据相似三角形的判定,分![]() ,
,![]() 两种情况讨论.
两种情况讨论.
解:(1)如图,过点A作AD⊥y轴于点D,
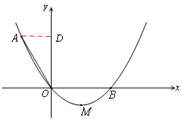
∵AO=OB=2,∴B(2,0).
∵∠AOB=1200,∴∠AOD=300,∴AD=1,OD=![]() .
.
∴A(-1,![]() ).
).
将A(-1,![]() ),B(2,0)代入
),B(2,0)代入![]() ,得:
,得:
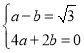 ,解得
,解得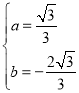 .
.
∴这条抛物线的表达式为![]() .
.
(2)过点M作ME⊥x轴于点E,
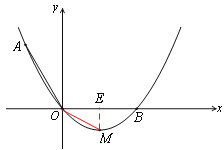
∵![]()
∴M(1,![]() ),即OE=1,EM=
),即OE=1,EM=![]() .
.
∴![]() .∴
.∴![]() .
.
∴∠AOM=∠AOB+∠EPM=150°.
(3)过点A作AH⊥x轴于点H ,
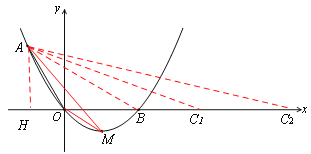
∵AH=![]() ,HB=HO+OB=3,
,HB=HO+OB=3,
∴tan∠ABH=![]() =
=![]()
∴∠ABH=30°,∠ABC=150°,
∴∠AOM=∠ABC.
∴要△ABC与△AOM相似,则必须:
①![]() ,或②
,或②![]() .
.
设点C的坐标为(c,0),则根据坐标和勾股定理,有
AO=2,OM=![]() ,BC=c-2,AB=
,BC=c-2,AB=![]() .
.
①由![]() 得,
得,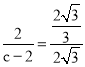 ,解得
,解得![]() .∴C1(4,0).
.∴C1(4,0).
②由![]() 得,
得,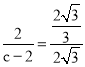 ,解得c=8.∴C2(8,0).
,解得c=8.∴C2(8,0).
综上所述,如果点C在x轴上,且△ABC与△AOM相似,则点C的坐标为(4,0)或(8,0).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目