Question

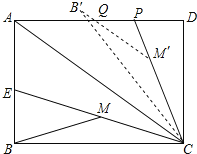
【题目】已知矩形ABCD中，AB=3，BC=4，CE平分∠ACB交AB于点E，M为CE的中点，连结BM，将△BCM绕点C顺时针旋转至△B′CM′，B′M′交AD于Q，延长CM′交AD于P，若PQ=PM′，则PQ= ．

Answer 1

【答案】﹣．

【解析】

试题分析：首先证明四边形ACM'Q是等腰梯形，设PQ=x，在直角△CDP中，根据勾股定理即可得到关于x的方程求得x的值．

解：设PQ=x，

∵CE平分∠ACB，

∴∠BCE=∠ACE，且=，

∵AB=3，BC=4，

∴AC=5，

∴，

∴BE=，AE=，

∴CE=，

∴CM=．

∵M是CE的中点，且△BCE是直角三角形，

∴BM=CM=EM，

∴∠CBM=∠BCM=∠ACE，

又△B'CM'是△BCM旋转得到，

∴△B'CM'≌△BCM．

∵PQ=P'M，

∴∠PM'Q=∠PQM'=2∠B'CM'=∠ACB．

∵四边形ABCD是矩形，

∴AD∥BC，

∴∠ACB=∠CAD，

∴∠PQM'=CAD，

∴AC∥B'M'，

∴∠PM'Q=∠ACP，

∴∠CAD=∠ACP，

∴四边形ACM'Q是等腰梯形，

∴AQ=CM'=，

∴PD=+x，

在直角△CDP中，根据勾股定理得：CP2=PD2+CD2，

（+x）2=（4﹣﹣x）2+9，另t=+x，则t2=（4﹣t）2+9，

∴t=，

∴+x=，

∴x=﹣，

∴PQ=﹣．

故答案是：﹣．