Question

【题目】如图，抛物线与轴交于A（-2，0），B（6，0）两点．

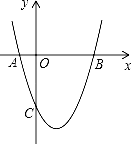
（1）求该抛物线的解析式；

（2）求该抛物线的对称轴以及顶点坐标；

（3）点P为y轴右侧抛物线上一个动点，若S△PAB=32，求出此时P点的坐标．

Answer 1

【答案】（1）二次函数解析式是（2）抛物线的对称轴顶点坐标（2，﹣16）；（3）点P的坐标为或时，

【解析】

试题分析：（1）根据抛物线与轴交于A（﹣2，0），B（6，0）两点，列出和的二元一次方程组，求出和的值即可；

把化成顶点坐标式为进而求出对称轴以及顶点坐标；

先求出AB的长，利用三角形的面积公式求出P的纵坐标，进而求出P点的坐标．

试题解析：（1）∵抛物线与轴交于A（﹣2，0），B（6，0）两点，∴，解得，∴二次函数解析式是

（2）∵∴抛物线的对称轴顶点坐标（2，﹣16）．

（3）设P的纵坐标为，

把代入解析式得，解得，，（负值舍去）把代入解析式得，解得，（负值舍去）∴点P的坐标为或时，