题目内容
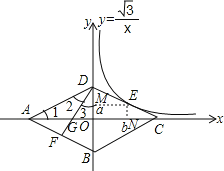
【题目】已知如图,菱形ABCD的四个顶点均在坐标轴上,对角线AC、BD交于原点O,DF⊥AB交AC于点G,反比例函数y=![]() (x>0)经过线段DC的中点E,若BD=4,则AG的长为( )
(x>0)经过线段DC的中点E,若BD=4,则AG的长为( )

A.![]() B.
B.![]() +2 C.2
+2 C.2![]() +1 D.
+1 D.![]() +1
+1
【答案】A
【解析】
试题分析:过E作y轴和x的垂线EM,EN,证明四边形MENO是矩形,设E(b,a),根据反比例函数图象上点的坐标特点可得ab=![]() ,进而可计算出CO长,根据三角函数可得∠DCO=30°,再根据菱形的性质可得∠DAB=∠DCB=2∠DCO=60°,∠1=30°,AO=CO=2
,进而可计算出CO长,根据三角函数可得∠DCO=30°,再根据菱形的性质可得∠DAB=∠DCB=2∠DCO=60°,∠1=30°,AO=CO=2![]() ,然后利用勾股定理计算出DG长,进而可得AG长.
,然后利用勾股定理计算出DG长,进而可得AG长.
解:过E作y轴和x的垂线EM,EN,
设E(b,a),
∵反比例函数y=![]() (x>0)经过点E,
(x>0)经过点E,
∴ab=![]() ,
,
∵四边形ABCD是菱形,
∴BD⊥AC,DO=![]() BD=2,
BD=2,
∵EN⊥x,EM⊥y,
∴四边形MENO是矩形,
∴ME∥x,EN∥y,
∵E为CD的中点,
∴DOCO=4![]() ,
,
∴CO=2![]() ,
,
∴tan∠DCO=![]() =
=![]() ,
,
∴∠DCO=30°,
∵四边形ABCD是菱形,
∴∠DAB=∠DCB=2∠DCO=60°,∠1=30°,AO=CO=2![]() ,
,
∵DF⊥AB,
∴∠2=30°,
∴DG=AG,
设DG=r,则AG=r,GO=2![]() ﹣r,
﹣r,
∵AD=AB,∠DAB=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,
∴∠3=30°,
在Rt△DOG中,DG2=GO2+DO2,
∴r2=(2![]() ﹣r)2+22,
﹣r)2+22,
解得:r=![]() ,
,
∴AG=![]() ,
,
故选:A.

 快捷英语周周练系列答案
快捷英语周周练系列答案【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?