��Ŀ����
����Ŀ����֪������y��x2��2ax+m��
��1����a��2��m����5ʱ���������ߵ���ֵ��
��2����a��2ʱ�����������������������������㣬������y������ƽ��k����λ���Ⱥõ��µ���������x��û�н��㣬���ж�k��ȡֵ�������˵�����ɣ�
��3����m��0ʱ��ƽ����y���ֱ��l�ֱ���ֱ��y��x����a��1���������߽���P��Q���㣮��ƽ��ֱ��l������ʹ��P��Q����x����·�����a��ȡֵ��Χ��
���𰸡���1��-9����2��k��0������������3��a��1��a����1
��������
(1)��a��2��m����5���������߽���ʽ�����������ߵ���ֵ��
(2)��a��2���룬���������������������������㣬����������x�ᡢy��ֱ���һ���������������x�ᡢy�ύ��ԭ�㣬�ֱ����m��ֵ��������y������ƽ��k����λ���ȣ��õ��µ���������x��û�н��㣬�г�����ʽ�������ж�k��ȡֵ��
(3)�������⣬��a����0��aС��0����������ۼ��ɵ�a��ȡֵ��Χ��
�⣺(1)��a��2��m����5ʱ��
y��x2��4x��5
����x��2��2��9
���������ߵ���СֵΪ��9��
(2)��a��2ʱ��
y��x2��4x+m
��Ϊ�������������������������㣬
�ٸ���������x�ᡢy��ֱ���һ������
���=16-4m=0��
��m=4��
��y��x2��4x+4=��x-2��2
��y������ƽ��k����λ���Ⱥõ��µ���������x��û�н��㣬
��k��0��
�ڸ���������x�ᡢy�ύ��ԭ�㣬
��m=0��
��y��x2��4x
�߰�����y������ƽ��k����λ���Ⱥõ��µ���������x��û�н��㣬
��y��x2��4x+k
��ʱ����0��
��16��4k��0
���k��4;
���ϣ�k��0ʱ��������y������ƽ��k����λ���Ⱥõ��µ���������x��û�н��㣻
(3)��m��0ʱ��y��x2��2ax
�����߿������ϣ���x�ύ������Ϊ��0��0����2a��0����a��0��
ֱ��l�ֱ���ֱ��y��x����a��1���������߽���P��Q���㣬
ƽ��ֱ��l������ʹ��P��Q����x����·���
����a��0ʱ����ͼ1��ʾ��
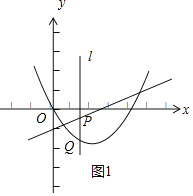
��ʱ����x��0ʱ��0��a+1��0�����a��1��
����a��0ʱ����ͼ2��ʾ��
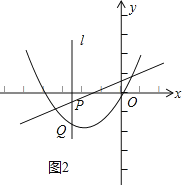
��ʱ����x��2aʱ��2a��a+1��0�����a����1��
���ϣ�a��1��a����1��