题目内容
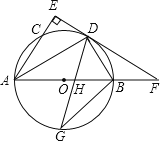
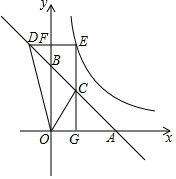
【题目】如图,已知直线l:y=﹣x+4分别与x轴、y轴交于点A,B,双曲线![]() (k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.
(k>0,x>0)与直线l不相交,E为双曲线上一动点,过点E作EG⊥x轴于点G,EF⊥y轴于点F,分别与直线l交于点C,D,且∠COD=45°,则k=_____.
【答案】8
【解析】
证明△ODA∽△CDO,则OD2=CDDA,而则OD2=(4﹣n)2+n2=2n2﹣8n+16,CD=![]() (m+n﹣4),DA=
(m+n﹣4),DA=![]() n,即可求解.
n,即可求解.
解:点A、B的坐标分别为(4,0)、(0,4),
即:OA=OB,∴∠OAB=45°=∠COD,
∠ODA=∠ODA,∴△ODA∽△CDO,
∴OD2=CDDA,
设点E(m,n),则点D(4﹣n,n),点C(m,4﹣m),
则OD2=(4﹣n)2+n2=2n2﹣8n+16,
CD=![]() (m+n﹣4),DA=
(m+n﹣4),DA=![]() n,
n,
即2n2﹣8n+16=![]() (m+n﹣4)×
(m+n﹣4)×![]() n,
n,
解得:mn=8=k,
故答案为8.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目