题目内容
【题目】如图,在坡顶B处的同一水平面上有一座纪念碑CD垂直于水平面,小明在斜坡底A处测得该纪念碑顶部D的仰角为45°,然后他沿着坡比i=5:12的斜坡AB攀行了39米到达坡顶,在坡顶B处又测得该纪念碑顶部的仰角为68°.求坡顶B到地面AE的距离和纪念碑CD的高度.(结果精确到1米,参考数据:sin68°=0.9,cos68°=0.4,tan68°=2.5)
【答案】解:过点B作BG⊥AE,垂足为点G,如图.
∵i=tan∠BAG= ![]() =5:12,
=5:12,
∴设BG=5k,则AG=12k,
在Rt△BAG中,由勾股定理得,AB=13k,
∴13k=39,解得k=3,
∴BG=15,
∴坡顶B到AE的距离为15米.
延长DC交AE于点F,
∵BC⊥DC,BC∥AE,
∴DF⊥AE,
∴四边形BCFG是矩形,CF=BG=15,BC=GF,
∵∠DAF=45°,
∴AF=DF,
设DC=x,则AF=36+GF,DF=x+15,即x+15=35+GF,
∴BC=GF=x﹣21,
在Rt△DBC中,tan∠DBC= ![]() ,即
,即 ![]() ≈2.5,
≈2.5,
解得x≈35,
答:坡顶B到地面AE的距离为15米,纪念碑CD的高度约为35米.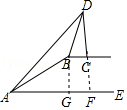
【解析】过点B作BG⊥AE,垂足为点G,如图.根据已知条件得到设BG=5k,则AG=12k,在Rt△BAG中,由勾股定理得,AB=13k,得到BG=15,于是得到坡顶B到AE的距离为15米.延长DC交AE于点F,根据平行线的性质得到DF⊥AE,根据矩形的性质得到AF=DF,设DC=x,则AF=36+GF,DF=x+15,得到BC=GF=x﹣21,根据三角函数的定义即可得到结论.
【考点精析】本题主要考查了关于坡度坡角问题和关于仰角俯角问题的相关知识点,需要掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA;仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】某校组织七年级全体学生举行了“汉字听写”比赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果,绘制成如下的图表.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |

根据以上信息完成下列问题:
(1)由统计表可知m+n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)已知该校七年级共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该年级本次听写比赛不合格的学生人数.