题目内容
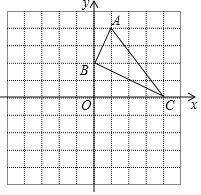
【题目】平面直角坐标系xOy(如图),抛物线y=﹣x2+2mx+3m2(m>0)与x轴交于点A、B(点A在点B左侧),与y轴交于点C,顶点为D,对称轴为直线l,过点C作直线l的垂线,垂足为点E,联结DC、BC.
(1)当点C(0,3)时,
①求这条抛物线的表达式和顶点坐标;
②求证:∠DCE=∠BCE;
(2)当CB平分∠DCO时,求m的值.
【答案】(1)y=﹣x2+2x+3;D(1,4);(2)证明见解析;(3)m=![]() ;
;
【解析】
(1)①把C点坐标代入y=﹣x2+2mx+3m2可求出m的值,从而得到抛物线解析式,
然后把一般式配成顶点式得到D点坐标;
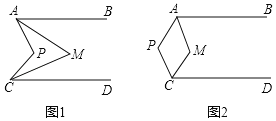
②如图1,先解方程﹣x2+2x+3=0得B(3,0),则可判断△OCB为等腰直角三角形得到∠
OBC=45°,再证明△CDE为等腰直角三角形得到∠DCE=45°,从而得到∠DCE=∠BCE;
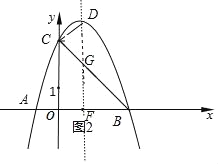
(2)抛物线的对称轴交x轴于F点,交直线BC于G点,如图2,把一般式配成顶点式得
到抛物线的对称轴为直线x=m,顶点D的坐标为(m,4m2),通过解方程﹣x2+2mx+3m2=0
得B(3m,0),同时确定C(0,3m2),再利用相似比表示出GF=2m2,则DG=2m2,接着证
明∠DCG=∠DGC得到DC=DG,所以m2+(4m2﹣3m2)2=4m4,然后解方程可求出m.
(1)①把C(0,3)代入y=﹣x2+2mx+3m2得3m2=3,解得m1=1,m2=﹣1(舍去),
∴抛物线解析式为y=﹣x2+2x+3;
∵![]()
∴顶点D为(1,4);
②证明:如图1,当y=0时,﹣x2+2x+3=0,解得x1=﹣1,x2=3,则B(3,0),
∵OC=OB,
∴△OCB为等腰直角三角形,
∴∠OBC=45°,
∵CE⊥直线x=1,
∴∠BCE=45°,
∵DE=1,CE=1,
∴△CDE为等腰直角三角形,
∴∠DCE=45°,
∴∠DCE=∠BCE;
(2)解:抛物线的对称轴交x轴于F点,交直线BC于G点,如图2,
![]()
∴抛物线的对称轴为直线x=m,顶点D的坐标为(m,4m2),
当y=0时,﹣x2+2mx+3m2=0,解得x1=﹣m,x2=3m,则B(3m,0),
当x=0时,y=﹣x2+2mx+3m2=3m2,则C(0,3m2),
∵GF∥OC,
∴![]() 即
即![]() 解得GF=2m2,
解得GF=2m2,
∴DG=4m2﹣2m2=2m2,
∵CB平分∠DCO,
∴∠DCB=∠OCB,
∵∠OCB=∠DGC,
∴∠DCG=∠DGC,
∴DC=DG,
即m2+(4m2﹣3m2)2=4m4,
∴![]()
而m>0,
∴![]()

 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案