题目内容
【题目】已知AB∥CD,AM平分∠BAP,CM平分∠PCD.
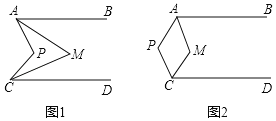
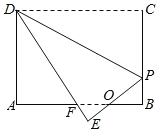
(1)如图①,当点P、M在直线AC同侧,∠AMC=60°时,求∠APC的度数;
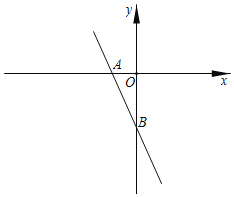
(2)如图②,当点P、M在直线AC异侧时,直接写出∠APC与∠AMC的数量关系.
【答案】(1)∠APC=120°;(2)∠APC=360°﹣2∠AMC.
【解析】
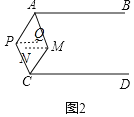
(1)延长AP交CD于点Q, 连接MP并延长到点R,根据角度关系推算即可.
(2) 过P作PQ∥AB于Q,MN∥AB于N,根据角度关系推算即可.
解:(1)如图1,延长AP交CD于点Q,则可得到∠BAP=∠AQC,
则∠APC=∠BAP+∠DCP=2(∠MAP+∠MCP),
连接MP并延长到点R,则可得∠APR=∠MAP+∠AMP,∠CPR=∠MCP+∠CMP,
所以∠APC=∠AMC+∠MAP+∠MCP,
所以∠APC=∠AMC+![]() ∠APC,
∠APC,
所以∠APC=2∠AMC=120°.
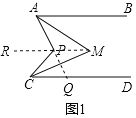
(2)如图2,过P作PQ∥AB于Q,MN∥AB于N,
则AB∥PQ∥MN∥CD,
∴∠APQ=180°﹣∠BAP,∠CPQ=180°﹣∠DCP,∠AMN=∠BAM,∠CMN=∠DCM,
∵AM平分∠BAP,CM平分∠PCD,
∴∠BAP=2∠BAM,∠DCP=2∠DCM,
∴∠APC=∠APQ+∠CPQ=180°﹣∠BAP+180°﹣∠DCP=360°﹣2(∠BAM+∠DCM)=360°﹣2(∠BAM+∠DCM)=360°﹣2∠AMC,即∠APC=360°﹣2∠AMC.

【题目】某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表
班级 | 中位数(分) | 众数(分) | 平均数(分) |
一班 | 85 | ||
二班 | 100 | 85 |
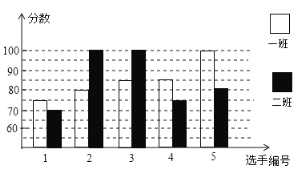
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知一班的复赛成绩的方差是70,请求出二班复试成绩的方差,并说明哪个班成绩比较稳定?