题目内容
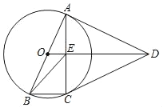
【题目】如图,AB为⊙O的直径,DA、DC分别切⊙O于点A,C,且AB=AD.
(1)求tan∠AOD的值.
(2)AC,OD交于点E,连结BE.
①求∠AEB的度数;
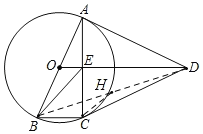
②连结BD交⊙O于点H,若BC=1,求CH的长.
【答案】(1)2;(2)①∠AEB=135°;②![]()
【解析】
(1)根据切线的性质可得∠BAD=90°,由题意可得AD=2AO,即可求tan∠AOD的值;
(2)①根据切线长定理可得AD=CD,OD平分∠ADC,根据等腰三角形的性质可得DO⊥AC,AE=CE,根据圆周角定理可求∠ACB=90°,即可证∠ABC=∠CAD,根据“AAS”可证△ABC≌△DAE,可得AE=BC=EC,可求∠BEC=45°,即可求∠AEB的度数;
②由BC=1,可求AE=EC=1,BE![]() ,根据等腰直角三角形的性质可求∠ABE=∠HBC,可证△ABE∽△HBC,可求CH的长.
,根据等腰直角三角形的性质可求∠ABE=∠HBC,可证△ABE∽△HBC,可求CH的长.
(1)∵DA是⊙O切线,∴∠BAD=90°.
∵AB=AD,AB=2AO,∴AD=2AO,∴tan∠AOD![]() 2;
2;
(2)①∵DA、DC分别切⊙O于点A,C,∴AD=CD,OD平分∠ADC,∴DO⊥AC,AE=CE.
∵AB是直径,∴∠ACB=90°,∴∠BAC+∠ABC=90°,且∠BAC+∠CAD=90°,∴∠ABC=∠CAD,且AB=AD,∠ACB=∠AED=90°,∴△ABC≌△DAE(AAS),∴CB=AE,∴CE=CB,且∠ACB=90°,∴∠BEC=45°=∠EBC,∴∠AEB=135°.
②如图,∵BC=1,且BC=AE=CE,∴AE=EC=BC=1,∴BE![]() .
.
∵AD=AB,∠BAD=90°,∴∠ABD=45°,且∠EBC=45°,∴∠ABE=∠HBC,且∠BAC=∠CHB,∴△ABE∽△HBC,∴![]() ,即
,即![]() ,∴CH
,∴CH![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】我市“木兰溪左岸绿道”工程已全部建成并投入使用,10公里的河堤便道铺满了彩色的透水沥青,堤岸旁的各类花草争奇斗艳,与木兰溪河滩上的特色花草相映成趣,吸引着众多市民在此休闲锻炼、散步观光.某小区随机调查了部分居民在一周内前往“木兰溪左岸绿道”锻炼的次数,并制成如图不完整的统计图表:
居民前往“木兰溪左岸绿道”锻炼的次数统计表
锻炼次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= .
(2)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(3)若该小区共有2000名居民,根据调查结果,估计该小区居民在一周内前往木兰溪左岸绿道”锻炼“4次及以上”的人数.

【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.





