Question

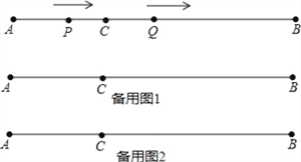
【题目】如图，已知正方形ABCD边长为1，点P是射线AD的上的一个动点，点A关于直线BP的对称点是点Q，设AP=x．

（1）求当D，Q，B三点在同一直线上时对应的x的值．

（2）当△CDQ为等腰三角形时，求x的值．

Answer 1

【答案】（1）；（2）， ， ．

【解析】分析: （1）求x，通常都是考虑勾股定理，选择直角三角形PDE，发现PE，DE，PD都可用x来表示，进而易得方程，求解即可．

（2）若△CDQ为等腰三角形，则边CD比为改等腰三角形的一腰或者底边．又Q点为A点关于PB的对称点，则AB＝QB，以点B为圆心，以AB的长为半径画弧，则Q点只能在弧AB上．若CD为腰，以点C为圆心，以CD的长为半径画弧，两弧交点即为使得△CDQ为等腰三角形（CD为腰）的Q点．若CD为底边，则作CD的垂直平分线，其与弧AC的交点即为使得△CDQ为等腰三角形（CD为底）的Q点．则如图所示共有三个Q点，那么也共有3个P点．作辅助线，利用直角三角形性质求之即可．

详解:

（1）连接DB，若Q点落在BD上，由AP=x，则PD=1﹣x，PQ=x．

∵∠PDQ=45°，

∴PD=PQ，

即1﹣x=x，

∴x=﹣1，

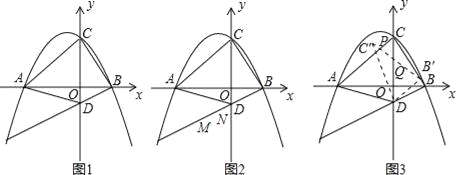
（2）①如图1，连接BQ1、CQ1，作PQ1⊥BQ1交AD于P，过点Q1，作EF⊥AD于E，交BC于F．

∵△BCQ1为等边三角形，正方形ABCD边长为1，

∴Q1F=Q1E=．

在四边形ABPQ1中，

∵∠ABQ1=30°，

∴∠APQ1=150°，

∴△PEQ1为含30°的直角三角形，

∴PE=Q1E=．

∵AE=，

∴x=AP=AE﹣PE=2﹣．

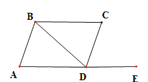
②如图2，连接BQ2，AQ2，过点Q2作PG⊥BQ2，交AD于P，连接BP，过点Q2作EF⊥CD于E，交AB于F．∵EF垂直平分CD，∴EF垂直平分AB，∴AQ2=BQ2．∵AB=BQ2，∴△ABQ2为等边三角形．在四边形ABQP中，∵∠BAD=∠BQP=90°，∠ABQ2=60°，∴∠ABP=30°，

∴x=AP=．

③如图4，连接BQ1，CQ1，BQ3，CQ3，过点Q3作BQ3⊥PQ3，交AD的延长线于P，连接BP，过点Q1，作EF⊥AD于E，此时Q3在EF上，不妨记Q3与F重合．

∵△BCQ1为等边三角形，△BCQ3为等边三角形，BC=1，

∴Q1Q2=，Q1E=，

∴EF=．

在四边形ABQ3P中

∵∠ABF=∠ABC+∠CBQ3=150°，

∴∠EPF=30°，

∴EP=EF=．

∵AE=，

∴x=AP=AE+PE=+2．

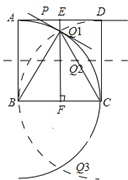
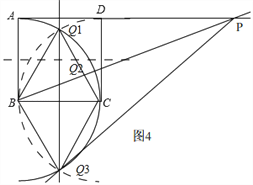
图1 图2

综上所述：△CDQ为等腰三角形时x的值为2﹣， ，2+．

点睛:本题第一问非常基础，难度较低．第二问因为动点的原因，思路不易找到，这里就需要做题时充分分析已知条件，尤其是新给出的条件．其中求边长是勾股定理的重要应用，是很重要的考点．第三问是一个难度非常高的题目，可以利用尺规作图的思想将满足要求的点Q找全．另外求解各个P点也是考察三角函数及勾股定理的综合应用，有着极高的难度．