Question

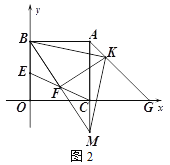
【题目】如图，在直角坐标系xOy中，已知A（6，0），B（8，6），将线段OA平移至CB，点D在x轴正半轴上（不与点A重合），连接OC，AB，CD，BD．

（1）写出点C的坐标；
（2）当△ODC的面积是△ABD的面积的3倍时，求点D的坐标；
（3）设∠OCD=α，∠DBA=β，∠BDC=θ，判断α、β、θ之间的数量关系，并说明理由．

Answer 1

【答案】
（1）

解：如图1，

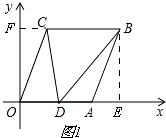
∵A（6，0），B（8，6），

∴FC=AE=8﹣6=2，OF=BE=6

∴C（2，6）；

（2）

解：设D（x，0），当△ODC的面积是△ABD的面积的3倍时，

若点D在线段OA上，

∵OD=3AD，

∴ ×6x=3× ×6（6﹣x），

∴x= ，

∴D（ ，0）；

若点D在线段OA延长线上，

∵OD=3AD，

∴ ×6x=3× ×6（x﹣6），

∴x=9，

∴D（9，0）

（3）

解：如图2．

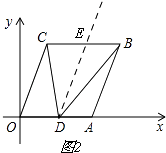
过点D作DE∥OC，

由平移的性质知OC∥AB．

∴OC∥AB∥DE．

∴∠OCD=∠CDE，∠EDB=∠DBA．

若点D在线段OA上，

∠CDB=∠CDE+∠EDB=∠OCD+∠DBA，

即α+β=θ；

若点D在线段OA延长线上，

∠CDB=∠CDE﹣∠EDB=∠OCD﹣∠DBA，

即α﹣β=θ．

【解析】（1）由点的坐标的特点，确定出FC=2，OF=6，得出C（2，6）；（2）分点D在线段OA和在OA延长线两种情况进行计算；（3）分点D在线段OA上时，α+β=θ和在OA延长线α﹣β=θ两种情况进行计算；