题目内容
【题目】在平面直角坐标系中,点A(m,m)在第一象限,且实数m满足条件:![]() ,ABy轴于B,ACx轴于C
,ABy轴于B,ACx轴于C
(1)求m的值;
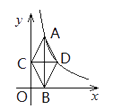
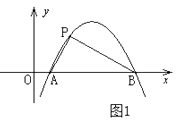
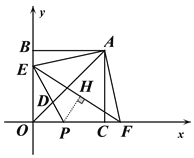
(2)如图1,BE=1,过A作AF⊥AE交x轴于F,连EF,D在AO上,且AD=AE,连接ED并延长交x轴于点P,求点P的坐标;
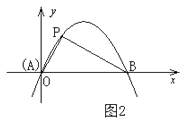
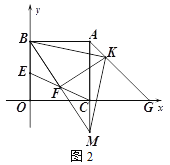
(3)如图2,G为线段OC延长线上一点,AC=CG,E为线段OB上一动点(不与O、B重合),F为线段CE的中点,若BF⊥FK交AG于K,延长BF、AC交于M,连接KM.请问∠FBK的大小是否变化?若不变,请求其值;若改变,求出变化的范围.

【答案】(1)7;(2)P(3,0);(3)∠FBK的大小不变,为45°,理由见解析.
【解析】
(1)由![]() 有意义可得m≥4,从而得到
有意义可得m≥4,从而得到![]() ,然后根据条件就可求出m的值.
,然后根据条件就可求出m的值.
(2)过点D作DH⊥x轴于点H,根据全等三角形的性质及勾股定理,就可得到点P的坐标.
(3)过K作KN⊥AC于N,KT⊥BA延长线于T.易证四边形ATKN是正方形,则有KT=KN,∠MTN=90°.易证△BEF≌△MCF,则有BF=MF,根据垂直平分线的性质可得KB=KM,从而可证到△TBK≌△NMK,进而得到答案.
(1)由![]() 得
得 ![]() ,
,![]() ,
,
∴![]() ,
,
原式化为:![]() ,
,
∴![]() ,
,
![]() .
.
(2)由(1)得A(7,7),
∵AB⊥y轴于B,AC⊥x轴于C,
∴AE=AC=7,
∴四边形ABOC为正方形,
∴BO=OC=7,∠BAC=90°,∠BOA=45°,
∵AF⊥AE,
∴∠EAF=90°,
∴∠BAE=∠CAF,
∴△ABE≌△ACF(ASA)
∴BE=CF,AE=AF,
∴∠AEF=45°,
∵AD=AE,
∴∠AED=∠ADE,
∴∠AEF+∠FEP=∠EOA+∠OEP,
∴∠OEP=∠FEP ,
过P作PH⊥EF于H,
∴OP=PH,
∴EO=EH,
在Rt△EOF中,EO=BO-BE=6,OF=OC+CF=8,
∴EF=![]() ,
,
设OP=PH=x,
在Rt△HPF中,HF=10-6=4,PF=8-x,
![]() ,即
,即![]() ,
,
解得![]() ,
,
∴P(3,0);
(3)∠FBK的大小不变,为45°。理由如下:
∵有正方形ABOC,
<>∴BO∥AC, ∠BAC=∠ACO=90°,∴∠EBF=∠CMF,∠BEF=∠MCF,
∵F为EC中点,
∴EF=CF,
∴△BEF≌△MCF(AAS),
∴BF=MF ,
∵BF⊥FK,
∴KB=KM ,
过K作KN⊥AC于N,KT⊥BA延长线于T,

∴∠T=∠KNM=90°,
∴四边形TANK为矩形,
∵AC=CG,
∴∠ANK=45°,
∴AN=NK,
∴矩形TANK为正方形,
∴TK=NK,
∴△TBK≌△NMK ,
∴∠TBK=∠NMK,
∴∠BKM=∠BAM=90°,
∴∠KBM=45°.

 阅读快车系列答案
阅读快车系列答案