题目内容
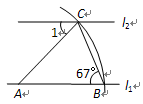
如图，直线l1∥l2，以直线l1上的点A为圆心、适当长为半径画弧，分别交直线l1、l2于点B、C，连接AC、BC．若∠ABC＝67º，则∠1＝
| A．23º | B．46º | C．67º | D．78º |
B
根据题意得：AB=AC，
∴∠ACB=∠ABC=67°，
∵直线l1∥l2，
∴∠2=∠ABC=67°，
∵∠1+∠ACB+∠2=180°，
∴∠ACB=180°-∠1-∠ACB=180°-67°-67°=46º．
故选B．
∴∠ACB=∠ABC=67°，
∵直线l1∥l2，
∴∠2=∠ABC=67°，
∵∠1+∠ACB+∠2=180°，
∴∠ACB=180°-∠1-∠ACB=180°-67°-67°=46º．
故选B．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
，
于
交
于
，已知
，则
（ ）
