��Ŀ����
����Ŀ����ͼ��
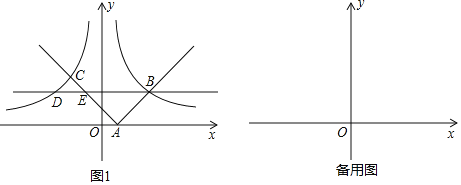
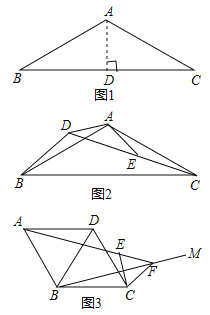
(1)�����ⱳ������ͼ1��������ABC��AB=AC,��BAC=120������![]() =________.
=________.
(2)��Ǩ��Ӧ�ã���ͼ2����ABC�͡�ABE���ǵ��������Σ���BAC=��DAE=120��,D,E,C������ͬ-��ֱ���ϣ�����BD�����߶�AD��BD��CD֮���������ϵʽ��
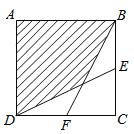
(3)����չ���죩��ͼ3��������ABCD�У���ABC=120�����ڡ�ABC��������BM������C����BM�ĶԳƵ�E������AE���ӳ���BM�ڵ�F������CE, CF����AE=4��CE=1����BF�ij�.
���𰸡�(1)![]() ��(2)CD=
��(2)CD=![]() AD+BD��(3)2
AD+BD��(3)2![]() .
.
��������
���ⱳ������AD��BC��D�����ݵ��������ε����ʵõ�BD=CD�������������ڽǺͶ��������ABC���������ҵĶ�����㼴�ɣ�
Ǩ��Ӧ�ã�֤����DAB�ա�EAC������ȫ�������ε����ʵõ�BD=CE�������ⱳ���õ�CD��AD��BD�Ĺ�ϵ��
��չ���죺��BG��AE��G������BE����BM��ֱƽ��CE���ɵá�EBF=��CBF���ٸ���AB=BE��BG��AE���ɵá�ABG=��EBG�������ó���GBF=![]() ��ABC=60�������ı���BCEG�У���á�CEG=120�����õ���CEF=60��������FE=FC���õ���EFC�ǵȱ������Σ���AE=4��EC=EF=1���ɵ�AG=GE=2��FG=3���ٸ�����Rt��BGF�У���BFG=30�������ɵõ�BF��
��ABC=60�������ı���BCEG�У���á�CEG=120�����õ���CEF=60��������FE=FC���õ���EFC�ǵȱ������Σ���AE=4��EC=EF=1���ɵ�AG=GE=2��FG=3���ٸ�����Rt��BGF�У���BFG=30�������ɵõ�BF��
���ⱳ������ͼ1����AD��BC��D��
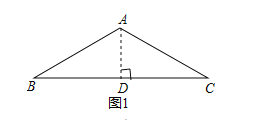
��AB=AC����BAC=120����
��BD=CD����ABC=30����
cosB=![]() ����
����![]() ��
��
��BC=![]() AB����
AB����![]() ��
��
�ʴ�Ϊ![]() ��
��
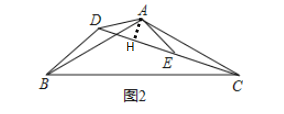
Ǩ��Ӧ�ã���ͼ2���ߡ�BAC=��DAE��
���DAB=��EAC��
����DAB����EAC��
 ��
��
���DAB�ա�EAC��SAS����
��BD=CE��
�����ⱳ����֪��DE=![]() AD��
AD��
��CD=DE+EC=![]() AD+BD��
AD+BD��
��չ���죺֤������ͼ3����BG��AE��G������BE��
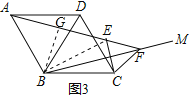
��E��C����BM�Գƣ�
��BC=BE��FE=FC��BF��CE��
���EBF=��CBF��
��������ABCD��AB=BC����ABC=120����
��AB=BE����BG��AE��
���ABG=��EBG��
���EBG+��EBF=![]() ��ABC=60����
��ABC=60����
���ı���BNEG�У���CEG=360��-90��-90��-60��=120����
���CEF=60������FE=FC��
���EFC�ǵȱ������Σ�
��AE=4��EC=EF=1��
��AG=GE=2��FG=3��
��Rt��BGF����BFG=30����
��BF=![]() =2
=2![]() ��
��

����Ŀ��С��ͬѧ�Ӽҵ�ѧУ��![]() ��
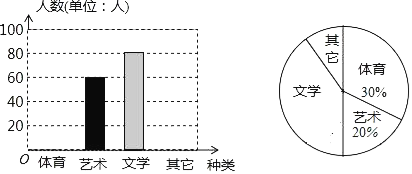
��![]() ������ͬ�Ĺ�����·��Ϊ�˽���߷��ڼ���������·�ϵĹ������Ӽص��ҵص���ʱ�������ÿ����·�����ѡȡ��500����εĹ��������ռ�����Щ��εĹ�������ʱ����λ�����ӣ������ݣ�ͳ�����£�
������ͬ�Ĺ�����·��Ϊ�˽���߷��ڼ���������·�ϵĹ������Ӽص��ҵص���ʱ�������ÿ����·�����ѡȡ��500����εĹ��������ռ�����Щ��εĹ�������ʱ����λ�����ӣ������ݣ�ͳ�����£�
��������ʱ Ƶ�� ������·�� |
|
|
|
| �ܼ� |
| 59 | 151 | 166 | 124 | 500 |
| 43 | 57 | 149 | 251 | 500 |
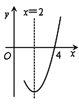
�ݴ˹��ƣ���߷��ڼ䣬����![]() ��·����ʱ������35�������ĸ���Ϊ__________����Ҫ��40����֮�ڵ���ѧУ��Ӧ����ѡ�����__________����
��·����ʱ������35�������ĸ���Ϊ__________����Ҫ��40����֮�ڵ���ѧУ��Ӧ����ѡ�����__________����![]() ��
��![]() ����·��
����·��