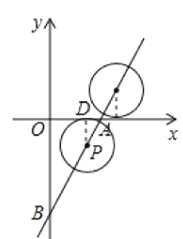
题目内容
【题目】己知:如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 是直线
是直线![]() 上一动点,⊙
上一动点,⊙![]() 的半径为2.
的半径为2.
(1)判断原点![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当⊙![]() 与
与![]() 轴相切时,求出切点的坐标.
轴相切时,求出切点的坐标.

【答案】(1)外部,理由见解析;(2)![]() 或
或 ![]() .
.
【解析】
(1)先求出OA,OB,进而根据三角形的面积公式求出![]() 到直线
到直线![]() 的距离
的距离![]() ,即可得出结论;
,即可得出结论;
(2)首先求得当⊙P与x轴相切时,且位于x轴下方时,点D的坐标,然后利用对称性可以求得当⊙P与x轴相切时,且位于x轴上方时,点D的坐标.
解(1)令x=0,![]() =
=![]()
∴![]() ,
,
令y=0,![]() =0,解得x=3
=0,解得x=3
∴![]()
∴AO=3,OB=![]()
![]() ,∠ABO=30
,∠ABO=30![]()
过![]() 作
作![]() D⊥AB,
D⊥AB,
设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
∴d=![]() =
=![]()
![]()
∴原点![]() 在
在![]() 的外部
的外部
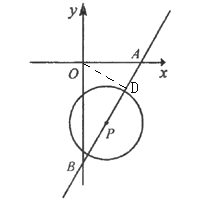
(2)如图,当⊙P与x轴相切时,且位于x轴下方时,设切点为D,
在PD⊥x轴,
∴PD∥y轴,
∴∠APD=∠ABO=30![]() ,
,
∴在Rt△DAP中,AD=DPtan∠DPA=2×tan30![]() =
=![]() ,
,
∴OD=OAAD=3-![]() ,
,
∴此时点D的坐标为:(3-![]() ,0);
,0);
当⊙P与x轴相切时,且位于x轴上方时,根据对称性可以求得此时切点的坐标为:(3+![]() ,0);
,0);
综上可得:当⊙P与x轴相切时,切点的坐标为: ![]() 或
或 ![]() .
.

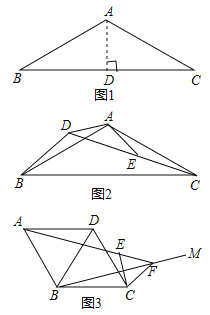
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,点E是线段AD上的一个动点,连接EC,线段EC绕点E顺时针旋转60°得到线段EF,连接DF、BF,已知AD=5cm,BC=8cm,设AE=xcm,DF=y1cm,BF=y2cm.小王根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小王的探究过程,请补充完整:
(1)对照下表中自变量x的值进行取点,画图,测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 |
y1/cm | 2.52 | 2.07 | 2.05 | 2.48 |
| 4.00 |
y2/cm | 1.93 | 2.93 | 3.93 | 4.93 | 5.93 | 6.93 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象:

(3)结合函数图象,解决问题:
①当AE的长度约为_______cm时,DF最小;
②当△BDF是以BF为腰的等腰三角形时,AE的长度约为______cm.