Question

【题目】已知一个三角形纸片ABC，面积为25，BC的长为10，∠B、∠C都为锐角，M为AB边上的一动点（M与A、B不重合），过点M作MN∥BC交AC于点N，设MN=x．
（1）用x表示△AMN的面积；
（2）△AMN沿MN折叠，使△AMN紧贴四边形BCNM（边AM、AN落在四边形BCNM所在的平面内），设点A落在平面BCNM内的点A′，△A′MN与四边形BCNM重叠部分的面积为y．
①用含x的代数式表示y，并写出x的取值范围．
②当x为何值时，重叠部分的面积y最大，最大为多少？

Answer 1

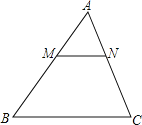
【答案】（1）S△AMN= ；（2）①-x2+10x-25（5＜x＜10），②当x=时，y最大，最大值为y最大=．

【解析】

（1）本题需先根据已知条件求出△AMN∽△ABC，再根据面积比等于相似比的平方的性质即可求出△AMN的面积．
（2）本题需先根据已知条件分两种情况进行讨论，当点A′落在四边形BCMN内或BC边上时和当点A′在四边形BCMN外时进行讨论，第一种情况很容易求出，第二种情况进行画图，连接AA′与MN交于点G与BC交于点F，再根据面积比等于相似比的平方的性质求出即可．再根据求出的式子，即可求出重叠部分的面积y的最大值来．

（1）∵MN∥BC，
∴△AMN∽△ABC，
∴，
∴，
∴S△AMN= ；
（2）①当点A′落在四边形BCMN内或BC边上时，0＜x≤5，

△A′MN与四边形BCNM重叠部分的面积为就是△A′MN的面积，
则此时y=S△A′MN=S△AMN=x2（0＜x≤5）
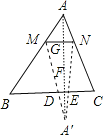
当点A′落在四边形BCMN外时，5＜x＜10，
△A′MN与四边形BCNM重叠部分的面积就是梯形MNED的面积，
连接AA′，与MN交于点G，与BC交于点F，
∵MN∥BC，
∴，
∴ ，

∴AG＝x，
∴AA′=2AG=x，
∴A′F=x-5，
∴，
∴，
∴S△A′DE=x2-10x+25，
∴此时y=x2-（x2-10x+25），
=-x2+10x-25（5＜x＜10），
②由①知：y=-x2+10x25，
∵a=-＜0，
∴该函数图象开口向下，当x=- ，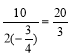
y取得最大值，ymax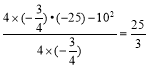＝ ．