题目内容
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.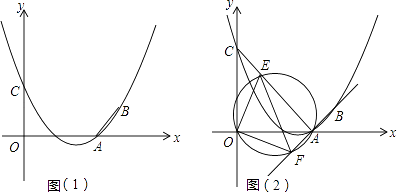
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.
【答案】
(1)
解:∵抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,
∴ ![]() ,
,
解得:  ,
,
∴y= ![]() x2﹣
x2﹣ ![]() x+3;
x+3;
∴点C的坐标为:(0,3)
(2)
解:假设存在,分两种情况:
①当△PAB是以A为直角顶点的直角三角形,且∠PAB=90°,
如图1,过点B作BM⊥x轴于点M,设D为y轴上的点,

∵A(3,0),B(4,1),
∴AM=BM=1,
∴∠BAM=45°,
∴∠DAO=45°,
∴AO=DO,
∵A点坐标为(3,0),
∴D点的坐标为:(0,3),
∴直线AD解析式为:y=kx+b,将A,D分别代入得:
∴0=3k+b,b=3,
∴k=﹣1,
∴y=﹣x+3,
∴y= ![]() x2﹣
x2﹣ ![]() x+3=﹣x+3,
x+3=﹣x+3,
∴x2﹣3x=0,
解得:x=0或3,
∴y=3,y=0(不合题意舍去),
∴P点坐标为(0,3),
∴点P、C、D重合,
②当△PAB是以B为直角顶点的直角三角形,且∠PBA=90°,
如图2,过点B作BF⊥y轴于点F,
由(1)得,FB=4,∠FBA=45°,
∴∠DBF=45°,
∴DF=4,
∴D点坐标为:(0,5),B点坐标为:(4,1),
∴直线BD解析式为:y=kx+b,将B,D分别代入得:
∴1=4k+b,b=5,
∴k=﹣1,
∴y=﹣x+5,
∴y= ![]() x2﹣
x2﹣ ![]() x+3=﹣x+5,
x+3=﹣x+5,
∴x2﹣3x﹣4=0,
解得:x1=﹣1,x2=4(舍),
∴y=6,
∴P点坐标为(﹣1,6),
∴点P的坐标为:(﹣1,6),(0,3);
(3)
解:如图3:作EM⊥AO于M,
∵直线AC的解析式为:y=﹣x+3,
∴tan∠OAC=1,
∴∠OAC=45°,
∴∠OAC=∠OAF=45°,
∴AC⊥AF,
∵S△FEO= ![]() OE×OF,
OE×OF,
OE最小时S△FEO最小,
∵OE⊥AC时OE最小,
∵AC⊥AF
∴OE∥AF
∴∠EOM=45°,
∴MO=EM,
∵E在直线CA上,
∴E点坐标为(x,﹣x+3),
∴x=﹣x+3,
解得:x= ![]() ,
,
∴E点坐标为( ![]() ,
, ![]() ).
).

【解析】(1)根据A(3,0),B(4,1)两点利用待定系数法求二次函数解析式;(2)从当△PAB是以A为直角顶点的直角三角形,且∠PAB=90°与当△PAB是以B为直角顶点的直角三角形,且∠PBA=90°,分别求出符合要求的答案;(3)根据当OE∥AB时,△FEO面积最小,得出OM=ME,求出即可.

 天天练口算系列答案
天天练口算系列答案【题目】某校组织学生到距离学校6千米的科技馆去参观,小华因事没能乘上学校的包车,于是准备在学校门口改乘出租车去科技馆,出租车收费标准有两种类型,如下表:
里程 | 甲类收费(元) | 乙类收费(元) |
3千米以下(包含3千米) | 7.00 | 6.00 |
3千米以上,每增加1千米 | 1.60 | 1.40 |
(1)设出租车行驶的里程为x千米(![]() 且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
且x取正整数),分别写出两种类型的总收费(用含x的代数式表示);
(2)小华身上仅有11元,他乘出租车到科技馆车费够不够请说明理由.



