题目内容
梯形ABCD中，AB∥DC，E、F分别是AD、BC的中点，DC=2，AB=4，设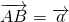
，则
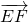可表示为
- A.
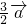
- B.
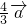
- C.
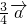
- D.
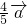
C
分析：根据梯形中位线定理可知EF=
（DC+AB）=3，则EF=
AB，在向量AB已知的情况下，可求出向量EF．
解答：∵AB∥DC，E、F分别是AD、BC的中点，
∴EF=（DC+AB）=3，
∴EF=AB．
∵，
∴=．
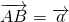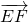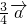故选C．
点评：本题考查了梯形中位线定理和平面向量的知识．梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半．由梯形中位线定理得到EF与AB的大小关系是解题的关键．
分析：根据梯形中位线定理可知EF=
（DC+AB）=3，则EF=AB，在向量AB已知的情况下，可求出向量EF．解答：∵AB∥DC，E、F分别是AD、BC的中点，
∴EF=
（DC+AB）=3，∴EF=
AB．∵
，∴
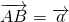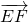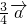=．故选C．
点评：本题考查了梯形中位线定理和平面向量的知识．梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半．由梯形中位线定理得到EF与AB的大小关系是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知在等腰梯形ABCD中，AB∥CD，AB＜CD，AB=10，BC=3．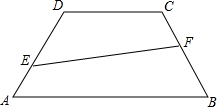
如图，等腰梯形ABCD中，AB∥DC，∠A=60°，AD=DC=10，点E，F分别在AD，BC上，且AE=4，BF=x，设四边形DEFC的面积为y，则y关于x的函数关系式是
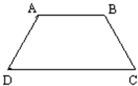5、如图，等腰梯形ABCD中，AB∥DC，AD=AB=BC=6，且∠D=60°，则DC=（ ）
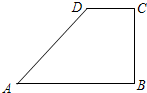如图，已知梯形ABCD中，AB∥CD，∠ABC=90°，CD=1．