题目内容
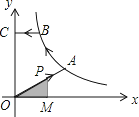
【题目】在平面直角坐标中，△ABC三个顶点坐标为A（﹣ 
，0）、B（ ，0）、C（0，3）． 
（1）求△ABC内切圆⊙D的半径．
（2）过点E（0，﹣1）的直线与⊙D相切于点F（点F在第一象限），求直线EF的解析式．
（3）以（2）为条件，P为直线EF上一点，以P为圆心，以2 
为半径作⊙P．若⊙P上存在一点到△ABC三个顶点的距离相等，求此时圆心P的坐标．
【答案】
（1）
解：连接BD，
∵B（ 
，0），C（0，3），
∴OB= ，OC=3，
∴tan∠CBO= 
= ，
∴∠CBO=60°
∵点D是△ABC的内心，
∴BD平分∠CBO，
∴∠DBO=30°，
∴tan∠DBO= 
，
∴OD=1，
∴△ABC内切圆⊙D的半径为1
（2）
解：连接DF，
过点F作FG⊥y轴于点G，
∵E（0，﹣1）
∴OE=1，DE=2，
∵直线EF与⊙D相切，
∴∠DFE=90°，DF=1，
∴sin∠DEF= 
，
∴∠DEF=30°，
∴∠GDF=60°，
∴在Rt△DGF中，
∠DFG=30°，
∴DG= 
，
由勾股定理可求得：GF= 
，
∴F（ ， ），
设直线EF的解析式为：y=kx+b，
∴ 
，
∴直线EF的解析式为：y= x﹣1
（3）
解：
∵⊙P上存在一点到△ABC三个顶点的距离相等，
∴该点必为△ABC外接圆的圆心，
由（1）可知：△ABC是等边三角形，
∴△ABC外接圆的圆心为点D
∴DP=2 
，
设直线EF与x轴交于点H，
∴令y=0代入y= x﹣1，
∴x= 
，
∴H（ ，0），
∴FH= ，
当P在x轴上方时，
过点P1作P1M⊥x轴于M，
由勾股定理可求得：P1F=3 ，
∴P1H=P1F+FH= 
，
∵∠DEF=∠HP1M=30°，
∴HM= P1H= 
，P1M=5，
∴OM=2 ，
∴P1（2 ，5），
当P在x轴下方时，
过点P2作P2N⊥x轴于点N，
由勾股定理可求得：P2F=3 ，
∴P2H=P2F﹣FH= 
，
∴∠DEF=30°
∴∠OHE=60°
∴sin∠OHE= 
，
∴P2N=4，
令y=﹣4代入y= x﹣1，
∴x=﹣ ，
∴P2（﹣ ，﹣4），
综上所述，若⊙P上存在一点到△ABC三个顶点的距离相等，此时圆心P的坐标为（2 ，5）或（﹣ ，﹣4）
【解析】（1）由A、B、C三点坐标可知∠CBO=60°，又因为点D是△ABC的内心，所以BD平分∠CBO，然后利用锐角三角函数即可求出OD的长度；（2）根据题意可知，DF为半径，且∠DFE=90°，过点F作FG⊥y轴于点G，求得FG和OG的长度，即可求出点F的坐标，然后将E和F的坐标代入一次函数解析式中，即可求出直线EF的解析式；（3）⊙P上存在一点到△ABC三个顶点的距离相等，该点是△ABC的外接圆圆心，即为点D，所以DP=2 ，又因为点P在直线EF上，所以这样的点P共有2个，且由勾股定理可知PF=3 ．本题是圆的综合问题，涉及圆的外接圆和内切圆的相关性质，圆的切线性质，锐角三角函数，一次函数等知识，综合程度较高，需要学生将各知识点灵活运用．
