题目内容
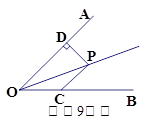
如图,点P是∠AOB的角平分线上一点,过点P作PC∥OA交OB于点C,若∠AOB=60°,OC=4,则点P到OA的距离PD等于 。

2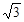
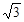
分析:在△OCP中,由题中所给的条件可求出OP的长,根据直角三角形的性质可知,在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半,故PD=
 OP.
OP.解答:
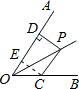
解:如图,过C点作CE⊥OA,垂足为E,
∵PC∥OA,PD⊥OA,垂足为D,∴PD=CE,
∵∠AOB=60°,OC=4,
在Rt△OCE中,CE=OC?sin60°=4×
 =2
=2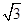 ,
,∴PD=CE=2
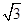 .
.点评:本题主要考查三角形的性质及计算技巧.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目

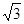 tan(α+20°)=1,你猜想锐角α的度数应是…( )
tan(α+20°)=1,你猜想锐角α的度数应是…( )  中,
中, ,如果
,如果 ,那么
,那么 的值是( )
的值是( )



 45°+
45°+ ×
× -tan
-tan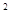 -ab-b
-ab-b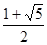 B、
B、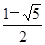 C、
C、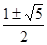 D、1
D、1 )0一(一1)2010
)0一(一1)2010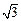 .求线段AD的长.
.求线段AD的长.