题目内容
在△ABC中,∠C=90°,a、b分别是∠A、∠B的对边,a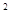 -ab-b
-ab-b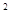 =0,则tanA等于
=0,则tanA等于
A、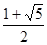 B、
B、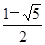 C、
C、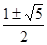 D、1
D、1
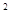 -ab-b
-ab-b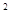 =0,则tanA等于
=0,则tanA等于A、
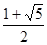 B、
B、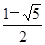 C、
C、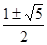 D、1
D、1A
根据a、b之间的等量关系式,可以求出 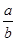 的值,进而得解.
的值,进而得解.
解:∵a、b满足a2-ab-b2=0,
等式两边同时除以b2得:(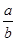 )2-
)2-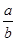 -1=0,
-1=0,
解得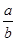 =
=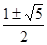 ,
,
∵tanA=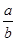 >0,
>0,
故tanA=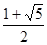 .
.
故选A.
本题考查了解直角三角形中三角函数的应用,求三角函数值转化成解一元二次方程的问题.
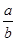 的值,进而得解.
的值,进而得解.解:∵a、b满足a2-ab-b2=0,
等式两边同时除以b2得:(
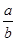 )2-
)2-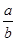 -1=0,
-1=0,解得
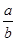 =
=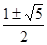 ,
,∵tanA=
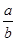 >0,
>0,故tanA=
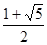 .
.故选A.
本题考查了解直角三角形中三角函数的应用,求三角函数值转化成解一元二次方程的问题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
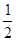 则sin
则sin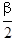 =__________,2tan2β=_________.
=__________,2tan2β=_________.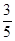 )
)
 ,求:
,求:
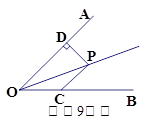
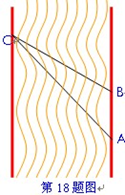
 =90°,三角形的角平分线CE和高AD相交于点F,过F作FG∥BC交AB于点G,求证:(1)AE=BG.(2)若∠
=90°,三角形的角平分线CE和高AD相交于点F,过F作FG∥BC交AB于点G,求证:(1)AE=BG.(2)若∠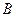 =30°,
=30°,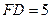 ,求四边形
,求四边形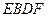 的面积.
的面积.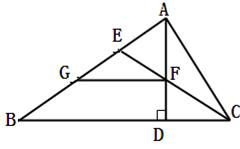
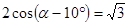 ,则锐角
,则锐角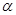 的度数是 °
的度数是 °