题目内容
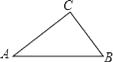
【题目】如图，从A地到B地的公路需经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°，因城市规划的需要，将在A、B两地之间修建一条笔直的公路．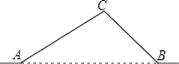 
（1）求改直的公路AB的长；
（2）问公路改直后比原来缩短了多少千米？（sin25°≈0.42，cos25°≈0.91，sin37°≈0.60，tan37°≈0.75）
【答案】
（1）解：作CH⊥AB于H．
在Rt△ACH中，CH=ACsin∠CAB=ACsin25°≈10×0.42=4.2（千米），
AH=ACcos∠CAB=ACcos25°≈10×0.91=9.1（千米），
在Rt△BCH中，BH=CH÷tan∠CBA=4.2÷tan37°≈4.2÷0.75=5.6（千米），
∴AB=AH+BH=9.1+5.6=14.7（千米）．
故改直的公路AB的长14.7千米
（2）解：在Rt△BCH中，BC=CH÷sin∠CBA=4.2÷sin37°≈4.2÷0.6=7（千米），
则AC+BC﹣AB=10+7﹣14.7=2.3（千米）．
答：公路改直后比原来缩短了2.3千米．
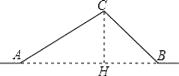
【解析】（1）作CH⊥AB于H．在Rt△ACH中，根据三角函数求得CH，AH，在Rt△BCH中，根据三角函数求得BH，再根据AB=AH+BH即可求解；（2）在Rt△BCH中，根据三角函数求得BC，再根据AC+BC﹣AB列式计算即可求解．
练习册系列答案
相关题目
