题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°. 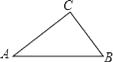
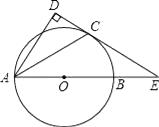
(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法) ①作AC的垂直平分线,交AB于点O,交AC于点D;
②以O为圆心,OA为半径作圆,交OD的延长线于点E.
(2)在(1)所作的图形中,解答下列问题. 点B与⊙O的位置关系是;(直接写出答案)
(3)若DE=2,AC=8,求⊙O的半径.
【答案】
(1)解:如图所示;
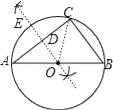
(2)点B在⊙O上
(3)解:∵OD⊥AC,且点D是AC的中点,
∴AD= ![]() AC=4,
AC=4,
设⊙O的半径为r,
则OA=OE=r,OD=OE﹣DE=r﹣2,
在Rt△AOD中,∵OA2=AD2+OD2,
即r2=42+(r﹣2)2,
解得r=5.
∴⊙O的半径为5
【解析】解: (2)连结OC,如图, ∵OD垂直平分AC,
∴OA=OC,
∴∠A=∠ACO,
∵∠A+∠B=90°,∠OCB+∠ACO=90°,
∴∠B=∠OCB,
∴OC=OB,
∴OB=OA,
∴点B在⊙O上;
所以答案是点B在⊙O上
(1)先作AC的垂直平分线,然后作⊙O;(2)通过证明OB=OA来判断点在⊙O上;(3)设⊙O的半径为r,在Rt△AOD中利用勾股定理得到r2=42+(r﹣2)2 , 然后解方程求出r即可.
【考点精析】根据题目的已知条件,利用点和圆的三种位置关系的相关知识可以得到问题的答案,需要掌握圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r.

 名校课堂系列答案
名校课堂系列答案【题目】某汽车行驶时油箱中余油量Q(L)与行驶时间t(h)的关系如表:
行驶时间t/h | 余油量Q/L |
1 | 42 |
2 | 34 |
3 | 26 |
4 | 18 |
5 | 10 |
(1)汽车行驶之前油箱中有汽油多少升?
(2)用行驶时间t的代数式表示余油量Q(直接写出答案);
(3)当t=![]() 时,求余油量Q的值.
时,求余油量Q的值.