题目内容
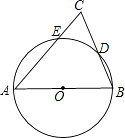
【题目】如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.求证: 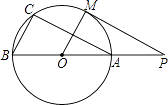
(1)△ABC∽△POM;
(2)2OA2=OPBC.
【答案】
(1)证明:∵直线PM切⊙O于点M,
∴∠PMO=90°,
∵弦AB是直径,
∴∠ACB=90°,
∴∠ACB=∠PMO,
∵AC∥PM,
∴∠CAB=∠P,
∴△ABC∽△POM;
(2)证明:∵△ABC∽△POM,
∴ ![]() ,
,
又AB=2OA,OA=OM,
∴ ![]() ,
,
∴2OA2=OPBC.
【解析】(1)因为PM切⊙O于点M,所以∠PMO=90°,又因为弦AB是直径,所以∠ACB=∠PMO=90°,再有条件弦AC∥PM,可证得∠CAB=∠P,进而可证得△ABC∽△POM;(2)由(1)可得 ![]() ,又因为AB=2OA,OA=OM;所以2OA2=OPBC.
,又因为AB=2OA,OA=OM;所以2OA2=OPBC.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

练习册系列答案
相关题目