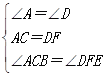��Ŀ����
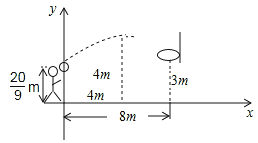
����Ŀ����ͼ���߳�Ϊa�ĵȱߡ�ACB�У�E�ǶԳ���AD��һ�����㣬��EC�����߶�EC�Ƶ�C��ʱ����ת60��õ�MC����DM�����ڵ�E�˶������У�DM����Сֵ��_____��

���𰸡�1.5
�����������������ȡAC���е�G������EG�����ݵȱ������ε����ʿɵ�CD=CG���������DCF=��GCE��������ת�����ʿɵ�CE=CF��Ȼ���������߽DZ���֤����DCF����GCEȫ�ȣ��ٸ���ȫ�������ζ�Ӧ����ȿɵ�DF=EG��Ȼ����ݴ��߶���̿ɵ�EG��ADʱ��̣��ٸ�����CAD=30����⼴�ɣ�
�⣺��ͼ��ȡAC���е�G������EG��
����ת��Ϊ60����
���ECD+��DCF=60����
���ߡ�ECD+��GCE=��ACB=60����
���DCF=��GCE��
��AD�ǵȱ���ABC�ĶԳ��ᣬ
��CD=![]() BC��
BC��
��CD=CG��
����CE��ת��CF��
��CE=CF��
����DCF����GCE��
 ��
��
���DCF�ա�GCE��SAS����
��DF=EG��
���ݴ��߶���̣�EG��ADʱ��EG��̣���DF��̣�
��ʱ�ߡ�CAD=![]() ��60��=30����AG=
��60��=30����AG=![]() AC=
AC=![]() ��6=3��
��6=3��
��EG=![]() AG=
AG=![]() ��3=1.5��
��3=1.5��
��DF=1.5��
�ʴ�Ϊ��1.5��

���㣺��ת�����ʣ��ȱ������ε����ʣ�
�����͡������
��������
19
����Ŀ���ֽ���ʽ��
(1) ![]() �� (2)9(m+n)2��16(m��n)2.
�� (2)9(m+n)2��16(m��n)2.
���𰸡���1��-2a(a-3)2 ;��2��-(7m-n)(m-7n).
�������������������ʽ�ֽ�ij��÷�������ȡ����ʽ������ʽ����ʮ����˷�������ֽⷨ.
�����������1��ԭʽ![]()
��2��ԭʽ![]()
![]()
![]()