Question

【题目】已知A（2，0），直线y＝(2－)x－2与x轴交于点F，与y轴交于点B，直线l∥AB且交y轴于点C，交x轴于点D，点A关于直线l的对称点为A′，连接AA′、A′D．直线l从AB出发，以每秒1个单位的速度沿y轴正方向向上平移，设移动时间为t．

（1）求点A′ 的坐标（用含t的代数式表示）；

（2）求证：AB＝AF；

（3）过点C作直线AB的垂线交直线y＝(2－)x－2于点E，以点C为圆心CE为半径作⊙C，求当t为何值时，⊙C与△AA′D三边所在直线相切？

Answer 1

【答案】（1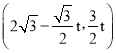）；（2）证明见解析；（3）1或.

【解析】试题分析：（1）由l∥AB得出∠ODC=∠OAB，再由点A（，0），求出∠ODC=∠OAB=30°，由点A关于直线l的对称点为A'，求出A'点的坐标（用t的代数式表示）；（2）通过点F的坐标，得出AF，在Rt△OAB中，OA=，OB=2，求出AB，得AB=AF；（3）先由直线l是点A和A'的对称轴得直线l是∠A'DA的平分线，即得点C到直线AD和A'D的距离相等，当⊙C与AD相切时，也一定与A'D相切，通过直角三角形求解．

试题解析：（1）∵直线与y轴交于点B，∴B（0， ）.

∵l∥AB，∴∠ODC=∠OAB.

∵A（，0），∴. ∴∠ODC=∠OAB=30°．

∵BC=t，∴OC=2t. ∴OD=. ∴AD= .

∵点A关于直线l的对称点为A'，∴A'D=AD= ，∠A'DA="60°." ∴△A'DA是等边三角形.

过点A'作A'H⊥AD于H，∴AH= ，A'H= .

∴A'点的坐标为．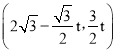

（2）∵直线与x轴交于点F ，∴F.

又A（，0），∴AF=4.

在Rt△OAB中，OA=，OB=2，∴AB=4.

∴AB=AF.

（3）分两种情况讨论：

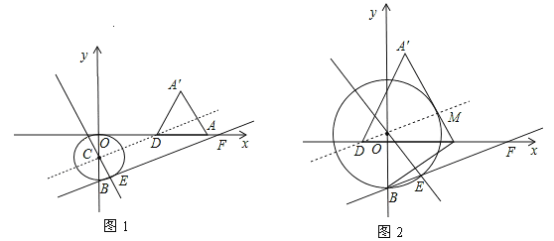
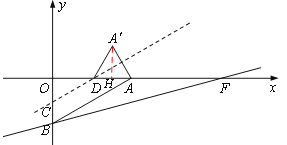
①如图1，当⊙C与AD（x轴）相切时，

∵直线l是点A和A'的对称轴，∴直线l是∠A'DA的平分线.

∴点C到直线AD和A'D的距离相等. ∴当⊙C与AD（x轴）相切时，也一定与A'D相切．

∵∠OAB=30°且AB=AF，∴∠ABF="15°." ∴∠CBF=75°．

∵CE⊥AB，∠OBA=60°，∴∠BCE="30°." ∴∠CEB=75°.

∴CB=CE．

∵⊙C与AD相切，∴OC="CE=CB." ∴t=1．

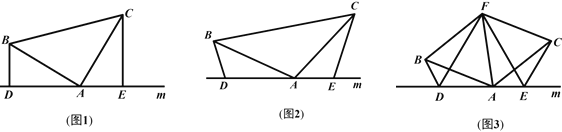
②如图2，当⊙C与AA'相切于点M时，CE=CB=CM，∴CM=t.

∵CM=DMCD，在Rt△OCD中，∠ODC=30°，OC=t2，∴CD=2t4.

∴，解得t=．

综上所述，当t=1或时，⊙C与△AA′D三边所在直线相切.