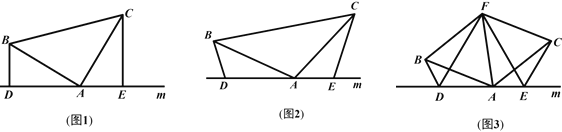
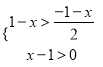题目内容
【题目】如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF,求证:AB=DE.

【答案】证明见解析.
【解析】试题分析:欲证明AB=DE,只要证明△ABC≌△DEF即可.
试题解析:∵AF=CD,
∴AC=DF,
∵BC∥EF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
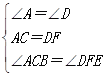 ,
,
∴△ABC≌△DEF(ASA),
∴AB=DE.
考点:全等三角形的判定与性质.
【题型】解答题
【结束】
25
【题目】如图, ![]() ,AE=BD,点D在AC边上,
,AE=BD,点D在AC边上, ![]() ,AE和BD相交于点O.
,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若![]() ,求BDE的度数.
,求BDE的度数.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)根据全等三角形的判定即可判断![]()
(2)由(1)可知: ![]() 根据等腰三角形的性质即可知
根据等腰三角形的性质即可知![]() 的度数,从而可求出
的度数,从而可求出![]() 的度数;
的度数;
试题解析:
证明: ![]() 和
和![]() 相交于点
相交于点![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
又![]()
![]() .
.
在![]() 和
和![]() 中,
中,
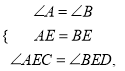
![]()
(2)![]()
![]() .
.
在![]() 中,
中,
![]()
![]() ,
,
![]() .
.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】高速路上因赶时间超速而频频发生交通事故,这样给自己和他人的生命安全带来直接影响,为了解车速情况,一名执法交警在高速路上随机测试了6个小轿车的车速情况记录如下:
车序号 | 1 | 2 | 3 | 4 | 5 | 6 |
车速(千米/时) | 100 | 95 | 106 | 100 | 120 | 100 |
则这6辆车车速的众数和中位数(单位:千米/时)分别是( )
A.100,95
B.100,100
C.102,100
D.100,103