题目内容
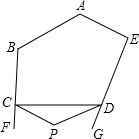 如图,五边形ABCDE中,∠BCD、∠EDC的外角分别是∠FCD、∠GDC,CP、DP分别平分∠FCD和∠GDC且相交于点P,若∠A=140°,∠B=120°,∠E=90°,∠P=
如图,五边形ABCDE中,∠BCD、∠EDC的外角分别是∠FCD、∠GDC,CP、DP分别平分∠FCD和∠GDC且相交于点P,若∠A=140°,∠B=120°,∠E=90°,∠P=考点:多边形内角与外角
专题:计算题
分析:根据多边形的内角和定理:(n-2)•180°,可得出∠BCD、∠EDC的和,从而得出相邻两外角和,然后根据角平分线及三角形内角和定理即可得出答案.
解答:解:多边形的内角和定理:(n-2)•180°=540°,
∴∠BCD+∠EDC=540°-140°-120°-90°=190°,
又∵CP和DP分别是∠BCD、∠EDC的外角平分线,
∴∠PCD+∠PDC=
(360°-∠BCD-∠EDC)=85°,
根据三角形内角和定理得:∠CPD=180°-85°=95°.
故答案为:95.
∴∠BCD+∠EDC=540°-140°-120°-90°=190°,
又∵CP和DP分别是∠BCD、∠EDC的外角平分线,
∴∠PCD+∠PDC=
| 1 |
| 2 |
根据三角形内角和定理得:∠CPD=180°-85°=95°.
故答案为:95.
点评:本题主要考查了多边形内角和定理、角平分线的性质、三角形内角和定理,比较综合,难度适中.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
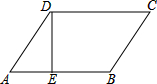 如图,在?ABCD中,DE⊥AB,E是垂足,∠C=40°,求∠A及∠CDE的度数.
如图,在?ABCD中,DE⊥AB,E是垂足,∠C=40°,求∠A及∠CDE的度数. 如图△ABC中,∠A=36°,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD交于点D,则∠D=
如图△ABC中,∠A=36°,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD交于点D,则∠D= 如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是
如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为6和8,那么点P到矩形的两条对角线AC和BD的距离之和是