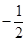题目内容
如图,在等腰三角形ABC中,AB=AC,O为AB上一点,以O为圆心、OB长为半径的圆交BC于点D,DE⊥AC交AC于点E.

小题1:求证:DE是⊙O的切线;
小题2:若⊙O与AC相切于点F,AB=AC=5,sinA= ,求⊙O半径的长度.
,求⊙O半径的长度.

小题1:求证:DE是⊙O的切线;
小题2:若⊙O与AC相切于点F,AB=AC=5,sinA=
 ,求⊙O半径的长度.
,求⊙O半径的长度.小题1:连OD
∵OB=OD
∴∠OBD=∠ODB
又∵AB=AC
∴∠ABC=∠ACB
∴∠ODB=∠ACB
∴OD//AC
∵DE⊥AC
∴∠AED=90°
∴ODE=90°
∴DE是⊙0的切线。…………………………………………………(4分)
小题2:如图,连OF,设半径为r
则DA=5-r OF⊥AC
∵
 ∴
∴


∴⊙O半径为
 ………………………………………………………………….(9分)
………………………………………………………………….(9分)(1)根据切线定理,只要证得 ODE=90°,即可知DE是⊙0的切线;
ODE=90°,即可知DE是⊙0的切线;
(2)根据 的正弦值列出方程可求得半径长。
的正弦值列出方程可求得半径长。
 ODE=90°,即可知DE是⊙0的切线;
ODE=90°,即可知DE是⊙0的切线;(2)根据
 的正弦值列出方程可求得半径长。
的正弦值列出方程可求得半径长。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




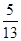 ,BC=24,则AC=__________.
,BC=24,则AC=__________.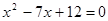 的两根,则这个三角形的斜边长是( )
的两根,则这个三角形的斜边长是( )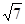
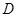 的正上方
的正上方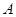 处测得月亮山山顶
处测得月亮山山顶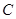 的俯角为
的俯角为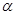 ,在月亮山山顶
,在月亮山山顶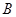 处测得东方山山顶
处测得东方山山顶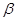 ,如图。已知
,如图。已知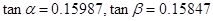 ,若飞机的飞行速度为180米/秒,则该飞机从
,若飞机的飞行速度为180米/秒,则该飞机从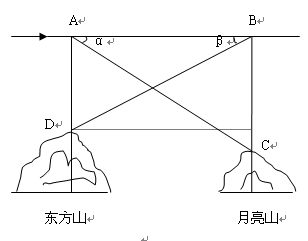
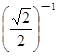 -2tan45°+(
-2tan45°+(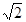 -1)0+22012×0.52012.
-1)0+22012×0.52012. 中,
中, ,
, ,
, ,那么
,那么 的值是( ▲ )
的值是( ▲ )



 ,
, ,
,
 ,
, ,
,
 为锐角时有
为锐角时有 ,由此可知:
,由此可知: ( )
( )