题目内容
如图,反比例函数 的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
(1)求一次函数的表达式;
(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量x的取值范围.
(1)y=x+1;(2)x<-3或0<x<2.
解析试题分析:(1)将A与B坐标分别代入反比例解析式求出m与n的值,确定出A与B坐标,再将两点代入一次函数解析式中求出k与b的值,即可确定出一次函数解析式;
(2)由A与B的横坐标,利用函数图象即可求出满足题意x的范围.
试题解析:(1)将A(m,3),B(-3,n)分别代入反比例解析式得:3=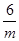 ,n=
,n=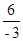 ,
,
解得:m=2,n=-2,
∴A(2,3),B(-3,-2),
将点A的坐标与点B的坐标代入一次函数解析式得: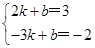 ,解得:k=1,b=1,
,解得:k=1,b=1,
则一次函数解析式为y=x+1;
(2)∵A(2,3),B(-3,-2),
∴由函数图象得:反比例函数值大于一次函数值的自变量x的取值范围为x<-3或0<x<2.
考点: 反比例函数与一次函数的交点问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的图象的一支.根据给出的图象回答下列问题:
的图象的一支.根据给出的图象回答下列问题:
 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:
 在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若
在第一象限内的图象分别交OA、AB于点C和点D,连结OD,若 ,
,
 (m为常数)图象的一支.
(m为常数)图象的一支.
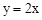 图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式. 上一点M(1,m)和双曲线
上一点M(1,m)和双曲线 上一点N(n,3).
上一点N(n,3). 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM.
 (x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.
(x>0)的图象经过点B,过点B作BC⊥x轴于点C,点P是该反比例函数图象上任意一点,过点P作PD⊥x轴于点D,点Q是线段AB上任意一点,连接OQ、CQ.