ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌЕШбќRtЁїABCжаЃЌЁЯABCЃН90ЁуЃЌABЃНBCЃЌЕуAЃЌBЗжБ№дкзјБъжсЩЯЃЎ
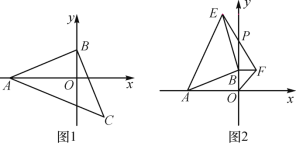
(1)ШчЭМ1ЃЌШєЕуCЕФКсзјБъЮЊ5ЃЌжБНгаДГіЕуBЕФзјБъ ЃЛ
(2)ШчЭМ2ЃЌШєЕуAЕФзјБъЮЊ(Ѓ6ЃЌ0)ЃЌЕуBдкyжсЕФе§АыжсЩЯдЫЖЏЪБЃЌЗжБ№вдOBЃЌABЮЊБпдкЕквЛЁЂЕкЖўЯѓЯозїЕШбќRtЁїOBFЃЌЕШбќRtЁїABEЃЌСЌНгEFНЛyжсгкЕуPЃЌЕБЕуBдкyжсЕФе§АыжсЩЯвЦЖЏЪБЃЌPBЕФГЄЖШЪЧЗёЗЂЩњИФБфЃПШєВЛБфЃЌЧѓГіPBЕФжЕЃЛШєБфЛЏЃЌЧѓPBЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП(1) (0ЃЌ5);(2)ВЛБфЃЌPBЃН3ЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉзїCDЁЭBOЃЌвзжЄЁїABOЁеЁїBCDЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШЕФаджЪМДПЩНтЬтЃЛ
ЃЈ2ЃЉзїEGЁЭyжсЃЌвзжЄЁїBAOЁеЁїEBGКЭЁїEGPЁеЁїFBPЃЌПЩЕУBG=AOКЭPB=PGЃЌМДПЩЧѓЕУPB![]() AOЃЌМДПЩНтЬтЃЎ
AOЃЌМДПЩНтЬтЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌзїCDЁЭBOгкDЃЎ
ЁпЁЯCBD+ЁЯABO=90ЁуЃЌЁЯABO+ЁЯBAO=90ЁуЃЌЁрЁЯCBD=ЁЯBAOЃЌ
дкЁїABOКЭЁїBCDжаЃЌЁп ЃЌ
ЃЌ
ЁрЁїABOЁеЁїBCDЃЈAASЃЉЃЌЁрCD=BO=5ЃЌЁрBЕузјБъЃЈ0ЃЌ5ЃЉЃЎ
ЙЪД№АИЮЊЃКЃЈ0ЃЌ5ЃЉЃЛ
ЃЈ2ЃЉШчЭМ3ЃЌзїEGЁЭyжсгкGЃЎ
ЁпЁЯBAO+ЁЯOBA=90ЁуЃЌЁЯOBA+ЁЯEBG=90ЁуЃЌЁрЁЯBAO=ЁЯEBGЃЌ
дкЁїBAOКЭЁїEBGжаЃЌЁп ЃЌ
ЃЌ
ЁрЁїBAOЁеЁїEBGЃЈAASЃЉЃЌЁрBG=AOЃЌEG=OBЃЎ
ЁпOB=BFЃЌЁрBF=EGЃЌ
дкЁїEGPКЭЁїFBPжаЃЌЁп ЃЌ
ЃЌ
ЁрЁїEGPЁеЁїFBPЃЈAASЃЉЃЌЁрPB=PGЃЌЁрPB![]() BG
BG![]() AO=3ЃЎ
AO=3ЃЎ