题目内容
【题目】如图,已知在平面直角坐标系 xOy 中,正比例函数 y=kx 与一次函数 y=x+b 的图象相交于点 A(4,3).过点 P(2,0)作 x 轴的垂线,分别交正比例函数的图象于点 B,交一次函数的图象于点 C, 连接 OC.
(1)求这两个函数解析式;
(2)求△OBC 的面积;
(3)在 x 轴上是否存在点 M,使△AOM 为等腰三角形? 若存在,直接写出 M 点的坐标;若不存在,请说明理由.

【答案】(1)y=![]() x; y=x+7;(2)
x; y=x+7;(2)![]() ;(3)存在,M(8,0),M(
;(3)存在,M(8,0),M(![]() ,0),M(
,0),M(![]() ,0),M(-
,0),M(-![]() ,0).
,0).
【解析】
(1)分别把A(4,3)代入y=kx,y=x+b,用待定系数法即可求解;
(2)先求出点B和点C的坐标,然后根据三角形的面积公式计算即可;
(3)分AO=AM时,AM=OM时,AO=OM时三种情况求解即可.
(1)把A(4,3)代入y=kx,得
4k=3,
∴k=![]() ,
,
∴y=![]() x;
x;
把A(4,3)代入y=x+b,得
-4+b=3,
∴b=7,
∴y=x+7;
(2)当x=2时,
y=![]() x=
x=![]() ,
,
y=x+7=5,
∴B(2,![]() ),C(2,5),
),C(2,5),
∴BC=5-![]() =
=![]() ,
,
∴△OBC 的面积=![]() OP·BC=
OP·BC=![]() ×2×
×2×![]() =
=![]() ;
;
(3)解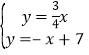 ,得
,得
![]() ,
,
∴A(4,3).
设M(x,0)
当AO=AM时,
![]() ,
,
解之得
x1=8,x2=0(舍去),
∴M(8,0);
当MA=OM时,
![]() ,
,
解之得
x =![]() ,
,
∴M(![]() ,0);
,0);
当AO=OM时,
![]() ,
,
解之得
x1=![]() ,x2=
,x2=![]() ,
,
∴M(![]() ,0)或M(-
,0)或M(-![]() ,0).
,0).
∴M(8,0),M(![]() ,0),M(
,0),M(![]() ,0),M(-
,0),M(-![]() ,0)时,△AOM 为等腰三角形.
,0)时,△AOM 为等腰三角形.

【题目】有这样一个问题:
探究函数![]() 的图象与性质.
的图象与性质.
小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)填表
| … |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | . . . |
| … | 3 | 2 |
|
| . . . |
(2)根据(1)中的结果,请在所给坐标系中画出函数![]() 的图象;
的图象;