题目内容
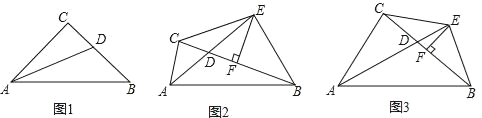
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.

(1)写出四边形![]() 的形状,并证明:
的形状,并证明:
(2)若四边形![]() 的面积为12,
的面积为12,![]() ,求
,求![]() .
.
【答案】(1)详见解析;(2)![]()
【解析】
(1)由“AAS”可证△AEF≌△DEC,可得AF=CD,由直角三角形的性质可得AD=BD=CD,由菱形的判定是可证ADBF是菱形.
(2)由题意可得S△ABC=S四边形ADBF=12,可得AC的长,由勾股定理可求BC的长.
解:解:(1)四边形ADBF是菱形,
理由如下:∵E是AD的中点,
∴AE=DE,
∵AF∥BC
∴∠AFE=∠DCE,且∠AEF=∠CED,AE=DE
∴△AEF≌△DEC(AAS)
∴AF=CD,
∵点D是BC的中点
∴BD=DC
∴AF=BD,且AF∥CD
∴四边形ADBF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=BD,
∴平行四边形ADBF是菱形
(2)∵四边形ADBF的面积为12,
∴S△ABD=6
∵D是BC的中点
∴S△ABC=12=![]() ×AB×AC
×AB×AC
∴12=![]() ×4×AC
×4×AC
∴AC=6,
∴BC=![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】某校七(1)班学生的平均身高是160厘米,下表给出了该班6名学生的身高情况(单位:厘米).
学 生 | A | B | C | D | E | F |
身 高 | 157 | 162 | 159 | 154 | 163 | 165 |
身高与平均身高的差值 | -3 | +2 | -1 | a | +3 | b |
(1)列式计算表中的数据a和b;
(2)这6名学生中谁最高?谁最矮?最高与最矮学生的身高相差多少?
(3)这6名学生的平均身高与全班学生的平均身高相比,在数值上有什么关系?(通过计算回答)