题目内容
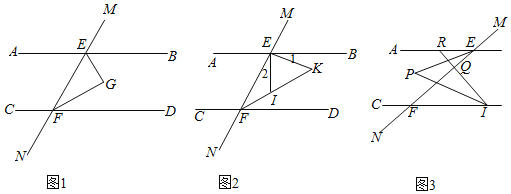
【题目】如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG绕点D顺时针旋转60°,得到正方形DE′F′G′,此时点G′在AC上,连接CE′,则CE′+CG′=( ) 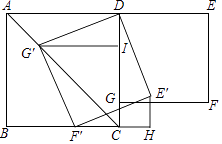
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:作G′I⊥CD于I,G′R⊥BC于R,E′H⊥BC交BC的延长线于H.连接RF′.则四边形RCIG′是正方形. ∵∠DG′F′=∠IGR=90°,
∴∠DG′I=∠RG′F′,
在△G′ID和△G′RF中,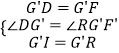 ,
,
∴△G′ID≌△G′RF,
∴∠G′ID=∠G′RF′=90°,
∴点F在线段BC上,
在Rt△E′F′H中,∵E′F′=2,∠E′F′H=30°,
∴E′H= ![]() E′F′=1,F′H=
E′F′=1,F′H= ![]() ,
,
易证△RG′F′≌△HF′E′,
∴RF′=E′H,RG′RC=F′H,
∴CH=RF′=E′H,
∴CE′= ![]() ,
,
∵RG′=HF′= ![]() ,
,
∴CG′= ![]() RG′=
RG′= ![]() ,
,
∴CE′+CG′= ![]() +
+ ![]() .
.
故选A.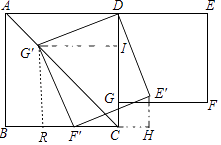
【考点精析】本题主要考查了正方形的性质和旋转的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了才能正确解答此题.

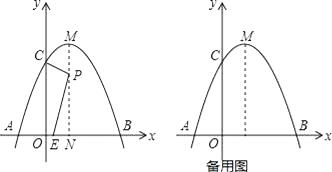
【题目】已知函数![]() ,它的图象犹如老师的打钩,因此人们称它为对钩函数(的一支).下表是
,它的图象犹如老师的打钩,因此人们称它为对钩函数(的一支).下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
请你根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行探究.
之间的变化规律,对该函数的图象与性质进行探究.
(1)如图,在平面直角坐标系![]() 中,已描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
中,已描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;

(2)请根据图象写出该函数的一条性质: .
(3)当![]() 时,
时,![]() 的取值范围为 ,则
的取值范围为 ,则![]() 的取值范围为 .
的取值范围为 .