题目内容
【题目】如图，高速公路旁有一个测速站M到公路l的距离MN为60米，一辆小汽车在公路l上行驶，测得此车从点A行驶到点B所有的时间为3秒，已知∠MAN=30°，∠MBN=60°．
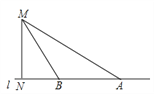
（1）计算此车从A到B的平均速度为每秒多少米（结果保留整数）；
（2）若此高速公路限速80千米/时，判断此车是否超速．（参考数据： 
≈1.41， 
≈1.73）
【答案】 (1)此车从A到B的平均速度为每秒23米；（2）此车已经超过限速．
【解析】试题分析: （1）根据题意需求AB长．由已知易知AB=BM，解直角三角形MNB求出BM即AB，再求速度；
（2）利用（1）中所求，与限制速度比较得结论．
试题解析:
（1）在Rt△AMN中，则AN=60
．
在Rt△BMN中，BN=60×
=20
．
∴AB=AN-BN=60
-20
=40
（m）．
则A到B的平均速度为： 
=
（米/秒）≈23（米/秒），
答：此车从A到B的平均速度为每秒23米；
（2）由题意可得：80千米/时=
米/秒≈22米/秒＜23米/秒．
答：此车已经超过限速．
点睛:此题主要考查了勾股定理得应用,将已知条件和所求结论中求解是解直角三角形的常规思路.
【题目】（6分）在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，表是活动进行中的一组统计数据：
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 68 | 109 | 136 | 345 | 368 | 701 |
摸到乒乓球的频率 | 0.68 | 0.73 | 0.68 | 0.69 | 0.70 | 0.70 |
（1）请估计：当n很大时，摸到白球的频率将会接近________；
（2）假如你去摸一次，你摸到白球的概率是_______，摸到黑球的概率是_______；
（3）试估算口袋中黑、白两种颜色的球各有多少只？