题目内容
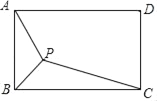
【题目】如图，矩形ABCD中，AB＝2
，BC＝6，P为矩形内一点，连接PA，PB，PC，则PA+PB+PC的最小值是（ ）
A. 4+3B. 2
C. 2+6D. 4
【答案】B
【解析】
将△BPC绕点C逆时针旋转60°，得到△EFC，连接PF、AE、AC，则AE的长即为所求．
解：将△BPC绕点C逆时针旋转60°，得到△EFC，连接PF、AE、AC，则AE的长即为所求．
由旋转的性质可知：△PFC是等边三角形，
∴PC=PF，
∵PB=EF，
∴PA+PB+PC=PA+PF+EF，
∴当A、P、F、E共线时，PA+PB+PC的值最小，
∵四边形ABCD是矩形，
∴∠ABC=90°，
∴tan∠ACB=
=
，
∴∠ACB=30°，AC=2AB=
，
∵∠BCE=60°，
∴∠ACE=90°，
∴AE=
=
.
故选B．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】探索与应用．先填写下表，通过观察后再回答问题：
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
（1）表格中x= ；y= ；
（2）从表格中探究a与
数位的规律，并利用这个规律解决下面两个问题：
①已知
≈3.16，则
≈ ；②已知
=1.8，若=180，则a= ；
（3）拓展：已知
，若
，则b= ．
